О формировании гомологических серий (рядов) химических соединений в многокомпонентных системах ионов химических элементов
О формировании гомологических серий (рядов) химических соединений в многокомпонентных системах ионов химических элементов
Аннотация
В работе рассмотрен способ расчета гомологических серий (рядов) химических соединений трех-, четырех- и пятикомпонентных систем ионов химических элементов в обобщенном виде. При представлении систем треугольником и треугольной пирамидой, в углах которых помещены ионы химических элементов, используются геометрические особенности этих геометрических фигур, что позволило выявить в системах закономерности изменения состава химических соединений, которые оказались членами гомологических серий. Расчетами показано, что гомологические серии могут развиваться только в сторону двухкомпонентных химических соединений. Показана невозможность формирования и развития гомологических серий в сторону трехкомпонентных химических соединений из-за невыполнения в этом случае одного из основных требований существования гомологических серий – неизменность гомологической разницы для обеих ветвей гомологической серии, для ветви химических соединений и для ветви заряженных кластеров.
1. Введение
В литературе известно крайне мало сведений о гомологических сериях (ГС) химических соединений (ХС). Из-за отсутствия закона формирования ГС опубликованы только экспериментально полученные формулы ГС многокомпонентных систем химических элементов (ХЭ): BamCum + nO3n – 1
, LanNinO3n – 1 ; Lan + 1NinO3n + 1, n = 1-5 ; Lan + 1NinO3n – 1, n = 7, 9, 13 и 30 ; La2n – 4Ni2O4n – 5, n = 5-8 , Fe2+nFe3+2mOn + 3m , Srn + 1TinO3n + 1, M+4Ti4+nO2(n + 1), где M+ ≡ Li+, Na+, K+, Rb+, Cs+ и n = 1-9 . Однако, следуя условию электронейтральности формул ХС, в приведенных в , , , формулах ГС должны присутствовать два разновалентных иона никеля, Ni2+ и Ni3+. Следовательно, исходя из этого, все формулы этих ГС должны относиться не к трехкомпонентным, а к четырехкомпонентным системам ионов.Для системы (Y-Ba-Cu-O), на наш взгляд, ошибочно считающейся четырехкомпонентной, опубликованы формулы ГС: Y2Ba4Cu6 + nO14 + n
и YnBamCum + n Oy, где (m = 2, 3, 5; n = 1, 2) . Так, с учетом электронейтральности и диспропорционирования ионов меди Сu3+→Сu2+ , на наш взгляд, формулу Y2Ba4Cu6 + nO14 + n следует представить так: Y2Ba4Cu6 + nO14 + n ≡ Y2Ba4 Cu2+4 + nCu3+2 O14 + n.Для системы (Tl3+-Ca2+-Ba2+-Cu2+-O2-) опубликованы три формулы ГС:
TlmBa2Can - 1CunO2(n + 1)m (m = 1, 2; n = 1, 2, 3)
и Tl1Ba2Can - 1CunO2n + 3 (n = 1, 2, 3) и Tl2Ba2Can - 1CunO2n + 4 (n =1, 2, 3) .Однако все выше указанные формулы ГС не опираются на какой-либо закон формирования ГС, т. к. его в те времена не существовало.
Тем не менее, в работах
, , , и работах , , впервые были заложены основы способа расчета ГС трехкомпонентных систем ионов ХЭ. В работах , , , идеи этого способа были распространены для четырех-, а в работах , , – для пятикомпонентных ГС.Следует обратить внимание на полное совпадение формулы ГС (M+-Ti4+-O2-), полученной расчетом в
, и полученной в на основе эксперимента, что однозначно доказывает достоверность впервые разработанного способа расчета ГС в работах , , , , , а также в , , , , и , .Формулирование Правила формирования многокомпонентных ГС на основе экспериментов (рентгеноструктурных, термодинамических и др.) практически неосуществимо, так как для этого потребуется огромное количество достоверных данных для различных систем, которые затем необходимо как-то обобщить. Поэтому предпринятая в вышеописанных работах попытка разработать Правило формирования ГС многокомпонентных ХС в обобщенном виде, на наш взгляд, может быть полезна для экспериментаторов.
Для решения задачи о расчете ГС системы ХЭ представлены их ионами, которые помещаются в углах треугольника или треугольной пирамиды. Использование геометрических особенностей этих фигур в работах
, , , , , а также в , , , , и , , , удалось выявить закономерности химического взаимодействия компонент системы ионов ХЭ, определяемые как ГС.В вышеописанных работах сформулировано Правило формирования ГС, основанное на протекании цепи чередующихся взаимодействий активированных атомных кластеров с ионами элементарных веществ, напоминающую «сплошь разветвленную цепную реакцию»
.Цель работы: рассмотреть возможность формирования и развития ГС в сторону трехкомпонентных ХС (ТХС) в четырех– и пятикомпонентных системах ионов ХЭ.
2. Обоснование способа расчета ГС
Известно, что фундаментальные свойства ХС-членов ГС изменяются закономерно за счет закономерного изменения состава и структуры кристаллической решетки гомологов , . В одной и той же ГС гомологи отличаются друг от друга составом на определенное число повторяющихся структурных единиц – гомологическую разность, что и определяет отличие кристаллической структуры гомологов на один и тот же фрагмент:
где ЗК – заряженные кластеры.
Формулы базовых четырехкомпонентных кластеров (ЧХСn(bas)) и базовых пятикомпонентных кластеров (ПХСn(bas)), с которых начинается расчет ГС, представляются в обобщенном виде так
, , , , и , , , , , :где 0 < t, r, w, v, n (bas) ≥ 1.
Химические реакции, характеризующие формирование ГС, которые развиваются в сторону ДХС, описаны в обобщенном виде в работах
, , , , , а также в , , , , и , . Однако при этом только для четырехкомпонентных , и пятикомпонентных , систем возникает вопрос: могут ли развиваться ГС в сторону ТХС? Рассмотрим эту проблему на примере четырехкомпонентной подсистемы (т. 5 - Aa+ - Cc-) на рисунках 1, 2 и пятикомпонентной подсистемы (т. 6 – т. 9 - Cc-) на рисунках 3, 4.3. Четырехкомпонентная система (Aa+-Bb+-Dd+-Cc–) и подсистема (Aa+-[BrdDwb](r + w)bd+-Сс–)
В четырехкомпонентной системе (Aa+- Bb+- Dd+- Cc-) серия химических взаимодействий характеризует образование базового кластера ЧХСn(bas) на рисунке 1:
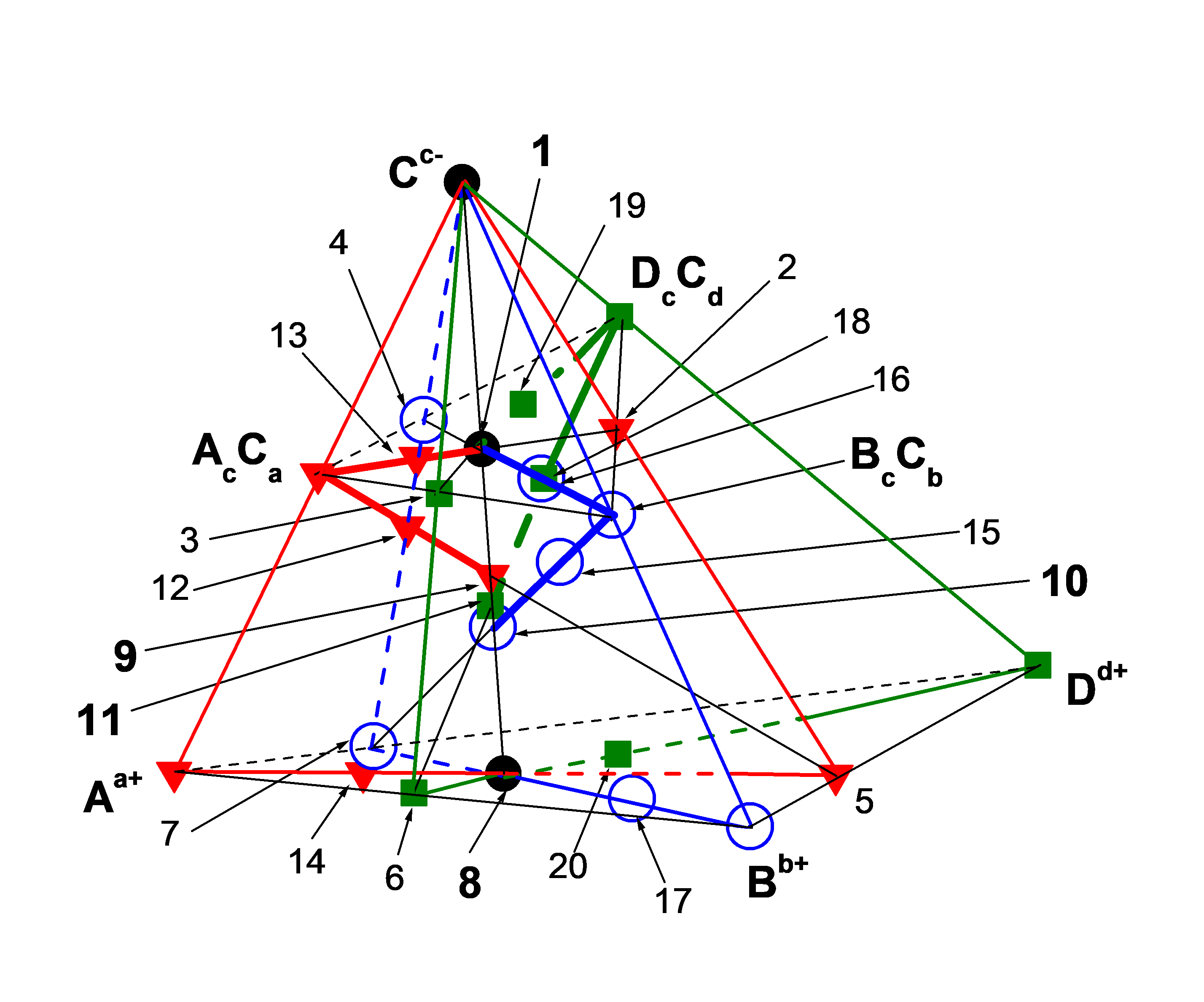
Рисунок 1 - Система (Aa+ – Bb+ – Dd+ – Cc-)
Примечание: т. 1 = ЧХСn(bas) = AtbdcBradcDwabcC(t + r + w)abd,
т. 2 = BrdcDwbcC(r + w)bd,
т. 3 = AtbcBracC(t + r)ab,
т. 4 = AtdcDwacC(t + w)ad,
т. 5 = [BrdDwb](r + w)bd+,
т. 6 = [AtbBra](t + r)ab+,
т. 7 = [AtdDwa](t + w)ad+,
т. 8 = ТЗКn(bas) = [(AtbdBradDwab](t + r + w)abd+,
т. 9 = ЧЗКn(bas) = [(AtbdcBradcDwabcCtabd](r + w)abdc+,
т. 10 = ЧЗКn(bas) = [(AtbdcBradcDwabcCrabd](t + w)abdc+,
т. 11 = ЧЗКn(bas) = [(AtbdcBradcDwabcCwabd](t + r)abdc+,
т. 12 = ЧЗКn(bas) + 1 = [(A(t + r + w)bdcBradcDwabcC(t + r + w)abd](r + w)abd+,
т. 13 = ЧХС n(bas) + 1 = A(t + r + w)bdcBradcDwabcC{t + 2(r + w)}abd,
т. 14 = ТЗКn(bas) + 1 = [(A(t + r + w)bdcBradcDwabc](t + r)abdc+,
т. 15 = ЧЗКn(bas) + 1 = [AtbdcB(t + r + w)adcDwabcC(t + r + w)abd](t + w)abdc+,
т. 16 = ЧХС n(bas) + 1 = AtbdcB(t + r + w)adcDwabcC(t + r + w)abd C{w + 2(t + w)}abd,
т. 17 = ТЗКn(bas) + 1 = [AtbdcB(t + r + w)adcDwabc]{r + 2(t + w)}abd+,
т. 18 = ЧЗКn(bas) + 1 = [AtbdcBradcD t + r + w)abcC(t + r + w)abd](t + r) abdc+,
т. 19 = ЧХС n(bas) + 1 = AtbdcBradcD( t + r + w)abcC(w + 2(t + r)abd,
т. 20 = ТЗКn(bas) + 1 = [AtbdcBradcD( t + r + w)abc]w + 2(t + r)abdc+
Рассмотрим возможно ли формирование ГС, которая развивалась бы в подсистеме (т. 5 - Aa+ - Cc-) в сторону трехкомпонентного ХС (ТХС) в виде (т. 2 = BrdcDwbcC( r + w)bd) с участием базового кластера (AtbdcBradcDwabcC(t + r + w)abd = ЧХСn(bas) = т. 1). Кластеры ЧХС и ЧЗК в искомой ГС должны располагаться на отрезках (т. 1 - т. 2) и (т. 21 - т. 2), соответственно, где (т. 21 = ЧЗКn(bas)) на рисунке 2.
bd+) – Aa+– Cc-}, направление {(т. 2 = BrdcDwbcC(r + w)bd)](/media/images/2025-01-09/60239ff8-a710-4317-a8cb-0da49f624e44.png)
Рисунок 2 - Подсистема {(т. 5 = [BrdDwb](r + w)bd+) – Aa+– Cc-}, направление {(т. 2 = BrdcDwbcC(r + w)bd)
Примечание: т. 1 = ЧХСn(bas) = AtbdcBradcDwabcC(t + r + w)abd),
т. 2 = BrdcDwbcC(r + w)bd,
т. 5 = [BrdDwb](r + w)bd+,
т. 8 = ТЗКn(bas) = [(AtbdBradDwab](t + r + w)abd+,
т. 9 = [(AtbdcBradcDwabcCtabd](r + w)abdc+,
т. 12 = ЧЗКn(bas) + 1 = [(A(t + r + w)bdcBradcDwabcC(t + r + w)abd](r + w)abdc+,
т. 13 = ЧХС n(bas) + 1 = A(t + r + w)bdcBradcDwabcC{t + 2(r + w)}abd,
т. 14 = ТЗКn(bas) + 1 = [(A(t + r + w)bdcBradcDwabc](t + r)abdc+,
т. 21 = ЧЗКn(bas) = [AtbdcBradcDwabcC(r + w)abd]tabdc+,
т. 22 = ЧЗКn(bas) + 1 = [At(r + w)bdcBr(t + r + w)adcDw(t + r + w)abcC(r + w)(t + r + w)abd]t(r + w)abdc+,
т. 23 = ЧХСn(bas) + 1 = At(r + w)bdcBr(t + r + w)adcDw(t + r + w)abcC(r + w)(2t + r + w)abd,
т. 24 = ТХСn(bas) + 1 = [At(r + w)bdcBr(t + r + w)adcDw(t + r + w)abc](r + w)(2t + r + w)abd+,
т. 25 = ЧЗКn(bas) + 2 = [At(r + w)bdcBr(2t + r + w)adcDw(2t + r + w)abcC(r + w)(2t + r + w)abd]t(r + w)abdc+,
т. 26 = ЧХСn(bas) + 2 = At(r + w)bdcBr(2t + r + w)adcDw(2t + r + w)abcC(r + w)(3t + r + w)abd,
т. 27 = ТХСn(bas) + 1 = [At(r + w)bdcBr(t + r + w)adcDw(t + r + w)abc](r + w)(2t + r + w)abd+
Формирование искомой ГС происходило бы согласно схеме:
4. Пятикомпонентная система (Aa+-Bb+-Dd+-Ff+-Cc–) и ее подсистема ([BrdDwb](r + w)bd+ - [AtfFva](t + v)af+ - Сс–)
В пятикомпонентной системе (Aa+- Bb+- Dd+-Ff+- Cc-) серия химических взаимодействий характеризует образование базового кластера ПХСn(bas) на рис. 3:
Взаимодействие базового кластера ПХСn(bas) с ионами Aa+ и Ff+ начинает формировать ГС-1 и ГС-2, которые развиваются в сторону АcСa и FcCf, соответственно. В результате, как описано в работах
, , в пирамиде выявляются подсистемы (т. 7 - Aa+ - Cc-) и (т. 8 - Ff+ - Cc-), где непосредственно формируются ГС-1 и ГС-2, соответственно (рис. 3). Появляющиеся кластеры ПЗКn(bas) в виде т. 11 и т. 12 при t ≠ r ≠ w ≠ v расположены на отрезке (т. 10 – Cc-) в разных местах (рис. 3), что свидетельствует о различии состава ПЗКn(bas) для разных направлений развития ГС. При t = r = w = v = 1 составы кластера ПЗКn(bas) для разных направлений развития ГС одинаковы.bd+-Сс–) в системе (Aa+-Bb+-Dd+-Ff+-Cc–)](/media/images/2025-01-09/8b10c9fb-0a3b-4ffa-a945-a9a34bebeda1.png)
Рисунок 3 - Подсистема (Aa+-Ff-[BrdDwb](r + w)bd+-Сс–) в системе (Aa+-Bb+-Dd+-Ff+-Cc–)
Примечание: т. 1 = ПХСn(bas) = AtbdfcBradfcDwabfcFvabdcC(t + r + w + v)abdf,
т. 2 = BrdfcDwbfcFvbdcC(r + w +v)bdf,
т. 3 = AtbdcBradcDwabcC(t + r + w)abd,
т. 4 = AtfcFvacC(t + v)af,
т. 5 = BrdcDwbcC(r + w)b,
т. 6 = [BrdDwb](r + w)bd+,
т. 7 = [BrdfDwbfFvbd](r + w + v)bdf+,
т. 8 = [AtbdBradDwab](t + r + w)abd+,
т. 9 = [AtfFva](t + v)af+,
т. 10 = ЧЗК n(bas) = [AtbdfBradfDwabfFvabd](t + r + w + v)abdf+,
т. 11 = (ПЗК n(bas) = [AtbdfcBradfcDwabfcFvabdcСtabdf](r + w + v)abdfc+) – ГС-1,
т. 12 = (ПЗК n(bas) = [AtbdfcBradfcDwabfFvabdcСrabdf](t + w + v)abdfc+) – ГС-2,
т. 13 = ПЗКn(bas) + 1 = ([A(t + r + w + v)bdfcBradfcDwabfcFvabdcC(t + r + w + v)abdf](r + w + v)abdfc+) – ГС-1,
т. 14 = ПХСn(bas) + 1 = (A(t + r + w + v)bdfcBradfcDwabfcFvabdcC{t + 2(r + w + v)}abdf ) – ГС-1,
т. 15 = ЧЗКn(bas) + 1 = ([A(t + r + w + v)bdfcBradfcDwabfcFvabdc](r + w + v)abdfc+ ) – ГС-1,
т. 16 = ПЗКn(bas) + 1 = [AtbdfcBradfcDwabfcF(t + r + w + v)abdcC(t + r + w + v)abdf](t + r + w)abdfc+,
т. 17 = ПХСn(bas) + 1 = (AtbdfcBradfcDwabfcF(t + r + w + v)abdcC{v + 2(t + r + w)}abdf ) – ГС-2,
т. 18 = ЧЗКn(bas) + 1 = ([AtbdfcBradfcDwabfcF(t + r + w + v)abdc](t + r + w)abdfc+ ) – ГС-2,
т. 19 = ПЗКn(bas) = [AtbdfcBradfcDwabfcFvabdcC(r + w)abdf](t + v)abdfc+,
т. 20 = ПЗКn(bas) + 1 = [(At(r + w)bdfcBr(t + r + w + v)adfcDw(t + r + w + v)abfcFv(r + w)abdcC(r + w)(t + r + w + v)abdf](t + v)(r + w)abdfc+,
т. 21 = ПХСn(bas) + 1 = At(r + w)bdfcBr(t + r + w + v)adfcDw(t + r + w + v)abfcFv(r + w)abdcC(r+ w)(2t + r + w + 2v)abdf,
т. 22 = ЧЗКn(bas) + 1 = [At(r + w)bdfBr(t + r + w + v)adfDw(t + r + w + v)abfFv(r + w)abd](r+ w)(2t + r + w + 2v)abdf+,
т. 23 = ПЗКn(bas) + 2 = [At(r + w)bdfcBr(2t + r + w + 2v)adfcDw(2t + r + w + 2v)abfcFv(r + w)abdcC(r+ w)(2t + r + w + 2v)abdf](t + v)(r + w)abdfc+,
т. 24 = ПХСn(bas) + 2 = At(r + w)bdfcBr(2t + r + w + 2v)adfcDw(2t + r + w + 2v)abfcFv(r + w)abdcC(r + w)(3t + r + w + 3v)abdf,
т. 25 = ЧЗКn(bas) + 2 = [At(r + w)bdfBr(2t + r + w + 2v)adfDw(2t + r + w + 2v)abfFv(r + w)abdf](r + w)(3t + r + w + 3v)abdf+,
т. 26 = ПЗК = [At(r + w)bdfcBr(t + v)adfcDw(t + v)abfcFv(r + w)abdcC(t + v)(r + w)abdf](t + v)(r + w)abdfc
В каждой из этих подсистем появляются другие подсистемы, которые, кроме подсистемы (Aa+ –-Ff+ – [BrdDwb](r + w)bd+ – Сс–), в работах
, на предмет формирования в них ГС подробно не рассматривались:Рассмотрим возможно ли формирование ГС, которые развивались бы в подсистеме (Aa+ – -Ff+ – [BrdDwb](r + w)bd+ – Сс–) и в ее подсистеме {([BrdDwb](r + w)bd+=т. 6) – ([AtfFva](t + v)af+=т. 9) – Сс–} в сторону ТХС в виде (т. 5 = BrdcDwbcC( r + w)bd) и (т. 4 = AtfcFvacC( r + w)af) с участием базового кластера (AtbdfcBradfcDwabfcFvabdcC(t + r + w + v)abdf = ПХСn(bas) = т. 1) на рисунках 3, 4.
Формирование ГС происходит согласно схеме:
4.1. Направление (т. 5 = BrdcDwbcC( r + w)bd) в подсистеме ([BrdDwb](r + w)bd+ - [AtfFva](t + v)af+ - Сс–)
Гомологи в искомой ГС должны находится на отрезках (т. 1 – т. 5) и (т. 19 – т. 5), где (т. 19 = ПЗКn(bas) = [AtbdfcBradfcDwabfcFvabdcC(r + w)abdf](t + v)abdfc+), формула которой определится ниже.
Для искомой ГС, которая развивалась бы в сторону (т. 5 = BrdcDwbcC( r + w)bd), кластер ПЗКn(bas) должен находиться в точке пересечения отрезков (т. 9 – т. 5) и (т. 10 – Сс-) на рисунке 4:
bd+) – (т. 9 = [AtfFva](t + v)af+) – Cc-}](/media/images/2025-01-10/58d3baec-f5ac-4c10-886c-f1245fbae20b.png)
Рисунок 4 - Подсистема {(т. 6 = [BrdDwb](r + w)bd+) – (т. 9 = [AtfFva](t + v)af+) – Cc-}
Примечание: т. 1 = ПХСn(bas) = AtbdfcBradfcDwabfcFvabdcC(t + r + w + v)abdf,
т. 4 = AtfcFvacC(t + v)af,
т. 5 = BrdcDwbcC(r + w)b,
т. 6 = [BrdDwb](r + w)bd+,
т. 9 = [AtfFva](t + v)af+,
т. 10 = ЧЗК n(bas) = [AtbdfBradfDwabfFvabd](t + r + w + v)abdf+,
т. 19 = ПЗКn(bas) = [AtbdfcBradfcDwabfcFvabdcC(r + w)abdf](t + v)abdfc+,
т. 20 = ПЗКn(bas) + 1 = [(At(r + w)bdfcBr(t + r + w + v)adfcDw(t + r + w + v)abfcFv(r + w)abdcC(r + w)(t + r + w + v)abdf](t + v)(r + w)abdfc+,
т. 21 = ПХСn(bas) + 1 = At(r + w)bdfcBr(t + r + w + v)adfcDw(t + r + w + v)abfcFv(r + w)abdcC(r+ w)(2t + r + w + 2v)abdf,
т. 22 = ЧЗКn(bas) + 1 = [At(r + w)bdfBr(t + r + w + v)adfDw(t + r + w + v)abfFv(r + w)abd](r+ w)(2t + r + w + 2v)abdf+,
т. 23 = ПЗКn(bas) + 2 = [At(r + w)bdfcBr(2t + r + w + 2v)adfcDw(2t + r + w + 2v)abfcFv(r + w)abdcC(r+ w)(2t + r + w + 2v)abdf](t + v)(r + w)abdfc+,
т. 24 = ПХСn(bas) + 2 = At(r + w)bdfcBr(2t + r + w + 2v)adfcDw(2t + r + w + 2v)abfcFv(r + w)abdcC(r + w)(3t + r + w + 3v)abdf,
т. 25 = ЧЗКn(bas) + 2 = [At(r + w)bdfBr(2t + r + w + 2v)adfDw(2t + r + w + 2v)abfFv(r + w)abdf](r + w)(3t + r + w + 3v)abdf+,
т. 26 = ПЗК = [At(r + w)bdfcBr(t + v)adfcDw(t + v)abfcFv(r + w)abdcC(t + v)(r + w)abdf](t + v)(r + w)abdfc+,
т. 27 = ПЗКn(bas) = [AtbdfcBradfcDwabfcFvabdcC(t + v)abdf](r + w)abdfc+,
т. 28 = ПЗКn(bas) + 1 = [At(t + r + w + v)bdfcBr(t + v)adfcDw(t + v)abfcFv(t + r + w + v)abdcC(t + v)(t + r + w + v)abdf](t + v)(r + w)abdfc+,
т. 29 = ПХСn(bas) + 1 = At(t + r + w + v)bdfcBr(t + v)adfcDw(t + v)abfcFv(t + r + w + v))abdcC(t + v)(t + 2r + 2w + v)abdf,
т. 30 = ЧЗКn(bas) + 1 = [At(t + r + w + v)bdfBr(t + v)adfDw(t + v)abfFv(t + r + w + v)abd](t + v)(t + 2r + 2w + v)abdf+,
т. 31 = ПЗКn(bas) + 2 = [At(t + 2r + 2w + v)bdfcBr(t + v)adfcDw(t + v)abfcFv(t + 2r +2w + v)abdcC(t + v)(t + 2r + 2w + v)abdf](t + v)(r + w)abdfc+,
т. 32 = ПХСn(bas) + 2 = At(t +2r +2w + v)bdfcBr(t + v)adfcDw(t + v)abfcFv(t +2r +2w + v)abdcC(t + v)(t + 3r + 3w + v)(abdf,
т. 33 = ЧЗКn(bas) + 2 = [At(t + 2r + 2w + v)bdfBr(t + v)adfDw(t + v)abfFv(t +2r +2w + v)abdf](t + v)(t + 3r + 3w + v )abdf+
Некоторый интерес представляет кластер в виде т. 26, расположенный на пересечении отрезков {(BrdcDwbcC(r + w)b = т. 5) - ([AtfFva](t + v)af+ = т. 9)} и {(AtfcFvacC(t + v)af =т. 4) – ([BrdDwb](r + w)bd+ =т. 6)} на рис. 3:
Как следует из (33), кластер в виде т. 26 не связан с базовым кластером (AtbdfcBradfcDwabfcFvabdcC(t + r + w + v)abdf = ПХСn(bas) = т. 1) взаимодействием с Сс- и, таким образом не является для последнего базовым ПЗКn(bas). Кроме этого, воображаемый (искомый) кластер ПЗКn(bas), связанный с (ПХСn(bas) = т.1) взаимодействием с Сс-, должен бы находиться на отрезке (т. 9 – т. 5), который определял бы направление развития искомой ГС, или, точнее, на пересечении отрезков (т. 10 – Сс-) и (т. 9 – т. 5) на рис. 3, что согласно (32) и (33) быть не может. Забегая вперед, аналогичное можно заключить, что в подсистеме {(т. 6 = [BrdDwb](r + w)bd+) – (т. 9 = = [AtfFva](t + v)af+) – Cc-} базовый кластер ПЗКn(bas), связанный с (ПХСn(bas) = т.1) взаимодействием с Сс-, должен бы находиться на отрезке (т. 4 – т. 6), который определял бы направление развития воображаемой (искомой) ГС, или, точнее, на пересечении отрезков (т. 10 – Сс-) и (т. 4 – т. 6) на рис. 3, чего также быть не может.
4.2. Направление (т. 4 = AtfcFvacC( r + w)af) в подсистеме ([BrdDwb](r + w)bd+ - [AtfFva](t + v)af+ - Сс–)
Гомологи в искомой ГС должны находится на отрезках (т. 1 – т. 4) и (т. 27 – т. 4), где (т. 27 = ПЗКn(bas) = [AtbdfcBradfcDwabfcFvabdcC(t + v)abdf](r + w)abdfc+), формула которого определится ниже.
Для искомой ГС, которая развивалась бы в сторону (т. 4 = AtfcFvacC(t + v)af), кластер ПЗКn(bas) должен находиться в точке пересечения отрезков (т. 6 – т. 4) и (т. 10 – Сс-):
В случае, когда (t = r = w = v = 1), кластер ПЗКn(bas) для обоих направлений развития ГС (т. 4 = AtfcFvacC(t + v)af) и (т. 5 = BrdcDwbcC( r + w)bd) был бы одним и тем же и он находился бы в точке пересечения отрезков (т. 9 – т. 5), (т. 6 – т. 4) и (т. 10 – Сс-), т.е. в т. 26, где согласно (32) кластер (т. 26= [AtbdfcBradfcDwabfcFvabdc](t + v)abdf+ = [AtbdfcBradfcDwabfcFvabdc](r + w)abdf+ ≡ [AbdfcBadfcDabfcFabdc]2abdf+) на рис. 4.
5. Заключение
Ранее в работах
, , , , , а также в , , , , и , , , для многокомпонентных систем ионов ХЭ разработан способ расчета формул ГС. Причем, ГС во всех случаях развивались в сторону только ДХС. Однако, в случае четырех- и пятикомпонентных систем вопрос развития ГС в сторону ТХС оставался открытым. Расчеты, проведенные для систем (Aa+- Bb+- Dd+- Cc–) и (Aa+- Bb+- Dd+-Ff+- Cc–) в данной работе показали, что в соответствии с уравнениями (14), (15), (28)-(31) и (42)-(45) одно из основных условий существования ГС (условие (1) – неизменность величины Δ, не выполняется. Из этого следует, что в системах (Aa+- Bb+- Dd+- Cc–) и (Aa+- Bb+- Dd+- Ff+- Cc-) не могут формироваться ГС, которые развиваются в сторону ТХС. Расчет, приведенный ранее в вышеописанных работах и в настоящей работе, показал, что ГС могут развиваться только в сторону ДХС, а в сторону ТХС – нет. Данный вывод важен еще и потому, что в литературе встречаются полученные на основе экспериментов формулы, приписываемые к ГС и противоречащие выводу настоящей работы.