ИНТЕРПРЕТАЦИЯ РЕОЛОГИЧЕСКИХ КРИВЫХ ПОЛИМЕРНЫХ РАСПЛАВОВ В ОБЛАСТИ ЛИНЕЙНОЙ ВЯЗКОУПРУГОСТИ
ИНТЕРПРЕТАЦИЯ РЕОЛОГИЧЕСКИХ КРИВЫХ ПОЛИМЕРНЫХ РАСПЛАВОВ В ОБЛАСТИ ЛИНЕЙНОЙ ВЯЗКОУПРУГОСТИ
Аннотация
Рассмотрены методы описания зависимости модуля потерь G" и модуля накопления G', от частоты сдвиговых колебаний в области линейной вязкоупругости в рамках структурной реологической модели. С помощью реологических уравнений структурной модели проведена аппроксимация отдельных участков реологических кривых G'(ω) и G''(ω). Уравнения описывают различные режимы осциллирующего течения, связанные с особенностями изменения структуры полимерного расплава под действием сдвига. Показано, что явление «срыва» величины модуля потерь G'' происходит при достижении некоторой постоянной величины модуля потерь G"SP вне зависимости от температуры расплава полимера.
1. Введение
Реологические кривые описывают зависимость реологических величин от внешних воздействий. Они являются основным источником сведений
, , о процессах стационарного и осциллирующего течения в структурированных жидкостях (суспензиях, эмульсиях, расплавах и растворах полимеров).Результаты динамических измерений позволяют получить зависимости модуля потерь G" и модуля накопления G' от циклической частоты ω. Такие измерения производят при малых амплитудах сдвиговых колебаний γ0, чтобы уменьшить воздействие сдвиговой деформации на структуру вещества. Предполагается, что в области линейной вязкоупругости структура вещества не изменяется при изменении частоты колебаний
.Полученные зависимости G'(ω) и G''(ω) рассматривают с помощью механических моделей пружины и демпфера, например, модели Максвелла и модели Кельвина – Фойхта . Обобщенная модель Максвелла использует при аппроксимации частотных зависимостей модулей так называемый релаксационный спектр, содержащий большое число коэффициентов. Насколько нам известно, реологические уравнения с двумя или тремя подгоночными коэффициентами не используются для описания зависимостей G'(ω) и G''(ω).
Качественное описание реологических кривых подразумевает разделение полного интервала частот на участки с определенным характером реологического поведения . В районе низких частот существует «вязкий или терминальный» район, где модуль потерь G" существенно больше модуля накопления G'. Для предельно низких частот справедливы функциональные зависимости G'' ~ ω G' ~ ω2. Район «перехода к течению» содержит точку пересечения (точку кроссовера), где G'' = G'. В последующем районе «вязкоэластичного или каучукоподобного» поведения доминирует упругость (G'' < G'), причем наклон кривой log G' (log ω) настолько мал, что говорят о существование G'-плато.
Величина модуля G" сначала уменьшается, а затем увеличивается с ростом частоты ω, образуя некое «псевдоплато». В районе «перехода» обычно наблюдается вторая точка пересечения (точка кроссовера). Величины G" и G' одновременно увеличиваются с ростом ω. В последующем районе «стеклования» величина G" становится больше величины G'. Модуль накопления G' имеет очень большую величину и слабо зависит от частоты.
Обычно на одном экспериментальном устройстве можно получить данные для одного или двух районов, поскольку «экспериментальное окно» является достаточно узким. Существование разных видов реологического поведения связывают с разными временами релаксации в соответствие с подходом Максвелла.
Предполагается, что характерные особенности кривых G'(ω) и G''(ω) связаны с реакцией системы на внешнюю периодическую деформацию, но сама структура вещества не изменяется на всем интервале частот.
В рамках структурной реологической модели , предполагается, что в области линейной вязкоупругости происходит изменение структуры вещества под действием сдвига. На отдельных интервалах частот существуют различные режимы течения, связанные с характером изменения структуры в результате изменения скорости сдвига γ0ω. Некоторые особенности реологических кривых в рамках структурного подхода нами рассматривались ранее , , .
В предлагаемой работе проводится анализ реологических кривых расплава полимера с помощью реологических уравнений структурной модели.
Целью представленной работы является проверка уравнений структурной реологической модели, предложенной нами ранее , , , для расплава полимера поли( — капролактан) при различных температурах. Особое внимание направлено на описание и объяснение явления «срыва» модуля потерь, т.е. выхода значения модуля потерь на плато в области высоких частот сдвиговых колебаний.
2. Методы исследования
Проведена аппроксимация реологических данных с помощью предложенных нами реологических уравнений методом нелинейной регрессии в пакете Excel. Нужно отметить, что вязкие и упругие свойства расплава при осциллирующем течении рассчитываются отдельно, в отличие от известных моделей, основанных на теоретических представлениях Максвелла.
Нами выбраны экспериментальные данные из работы , полученные для промышленного образца полимера поли( – капролактан) — алифатический полиэфир, используемого для производства гибкой упаковки. Промышленная марка полимера Capa ® 6800.
Вязкое поведение можно описать в рамках структурной модели , , используя реологические уравнения для двух режимов осциллирующего течения на отдельных участках реологической кривой. Каждому режиму соответствует определенное изменение структуры вещества, в данном случае разрушение и формирование зацеплений между макромолекулами в расплаве полимера. Если под действием сдвига зацепления разрушаются (но не формируются), то уравнение для модуля потерь имеет вид :
Поскольку , то можно записать уравнение для динамической вязкости:
Здесь коэффициент g' показывает степень агрегации частиц или прочность зацеплений макромолекул, коэффициент χ' указывает на тенденцию образования рыхлых агрегатов частиц или ассоциатов макромолекул, коэффициент описывает вязкость, возникающую за счет обтекания отдельных (индивидуальных) частиц или макромолекул. Используя кинетическое уравнение разрушения/формирования ассоциатов макромолекул, получим значения коэффициентов, присутствующих в уравнении (1):
. Величина N равна количеству частиц или макромолекул в единице объема, B' – некоторый коэффициент, не зависящий от частоты колебаний.
Коэффициенты кинетического уравнения имеют следующий смысл:
k'2 — константа скорости формирования агрегатов при столкновениях частиц;
k'0 — константа скорости спонтанного разрушения агрегатов, например, в результате теплового движения;
k'1 — константа скорости разрушения агрегата под действием растягивающих гидродинамических сил;
k'3 — константа скорости формирования агрегатов частиц из одиночных частиц под действием сдвига.
Если при столкновениях между частицами или макромолекулами возникают новые контакты или зацепления, то формируются новые агрегаты частиц или ассоциаты макромолекул. Этот процесс идет одновременно с разрывом контактов или зацеплений.
Реологическое уравнение для этого режима осциллирующего течения имеет вид:
где:
Коэффициент ΔG''1/2 является отрицательным, если k'0 > k'2, и положительным, если k0 < k2. Если то реологическое поведение похоже на «ньютоновское» с практически постоянным значением динамической вязкости
.
В районе высоких частот может наблюдаться явление «срыва», когда величина G'' увеличивается с увеличением частоты значительно медленнее предсказанного и постепенно выходит на «плато» с практически постоянной величиной G''SP.
3. Результаты и обсуждение
Рассмотрим зависимость модуля потерь расплава полимера поли(ε-капролактан) от частоты при разных температурах (рис. 1–5). При самых низкой температуре 62 ºС экспериментальная кривая может быть разделена на две части (рис. 1). В области низких частот (от 0,06 с-1 до 3 с-1) экспериментальные данные хорошо аппроксимируются уравнением (1). Пять точек в районе наиболее высоких частот демонстрируют практически постоянное значение G''SP ≈ 308 025 Па, что можно отнести к явлению «срыва» модуля потерь G''. Справедливость уравнения (1) подтверждается на графике в корневых координатах, построенного для интервала низких частот (рис. 1б).
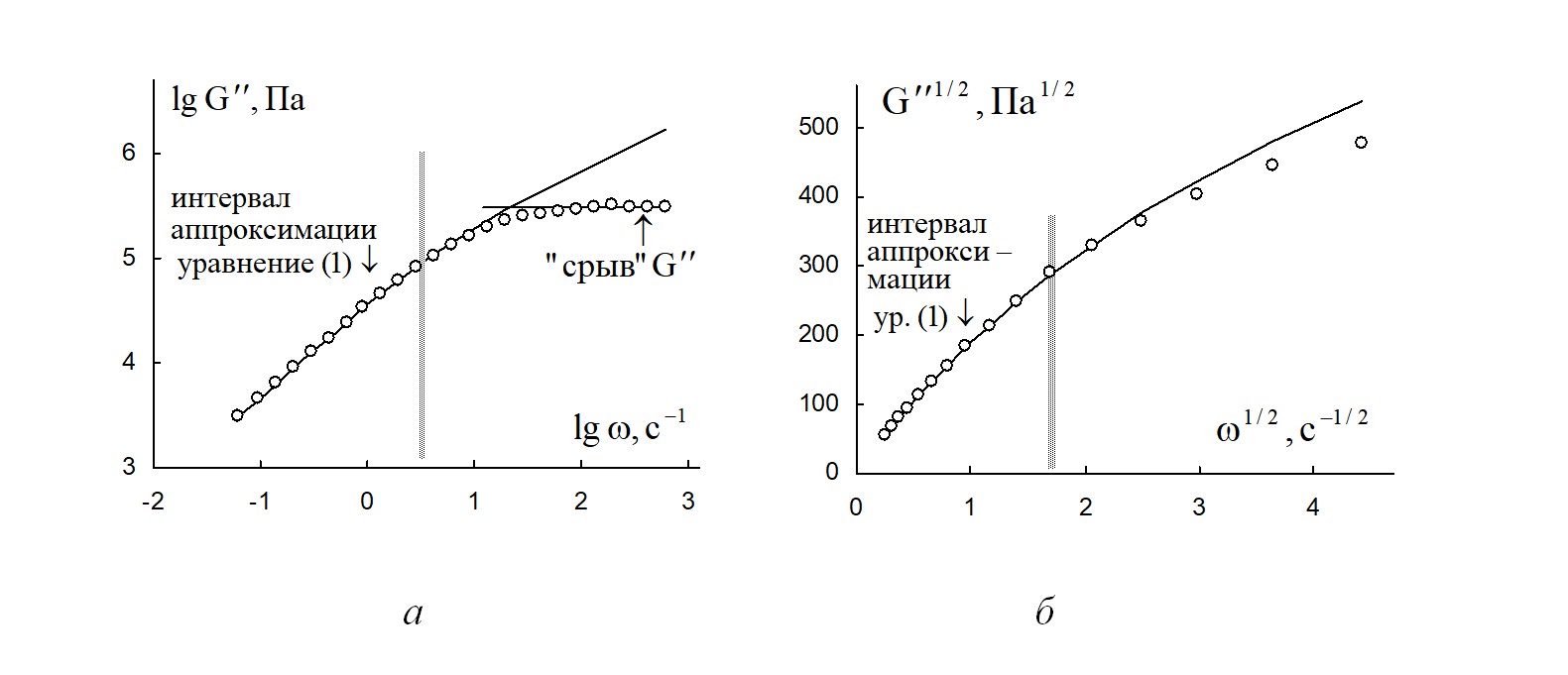
Рисунок 1 - Зависимость модуля потерь расплава полимера поли(ε-капролактан) от циклической частоты при температуре 62 ºС
Примечание: а – в двойных логарифмических координатах; б – в корневых координатах на интервале до 20 с-1
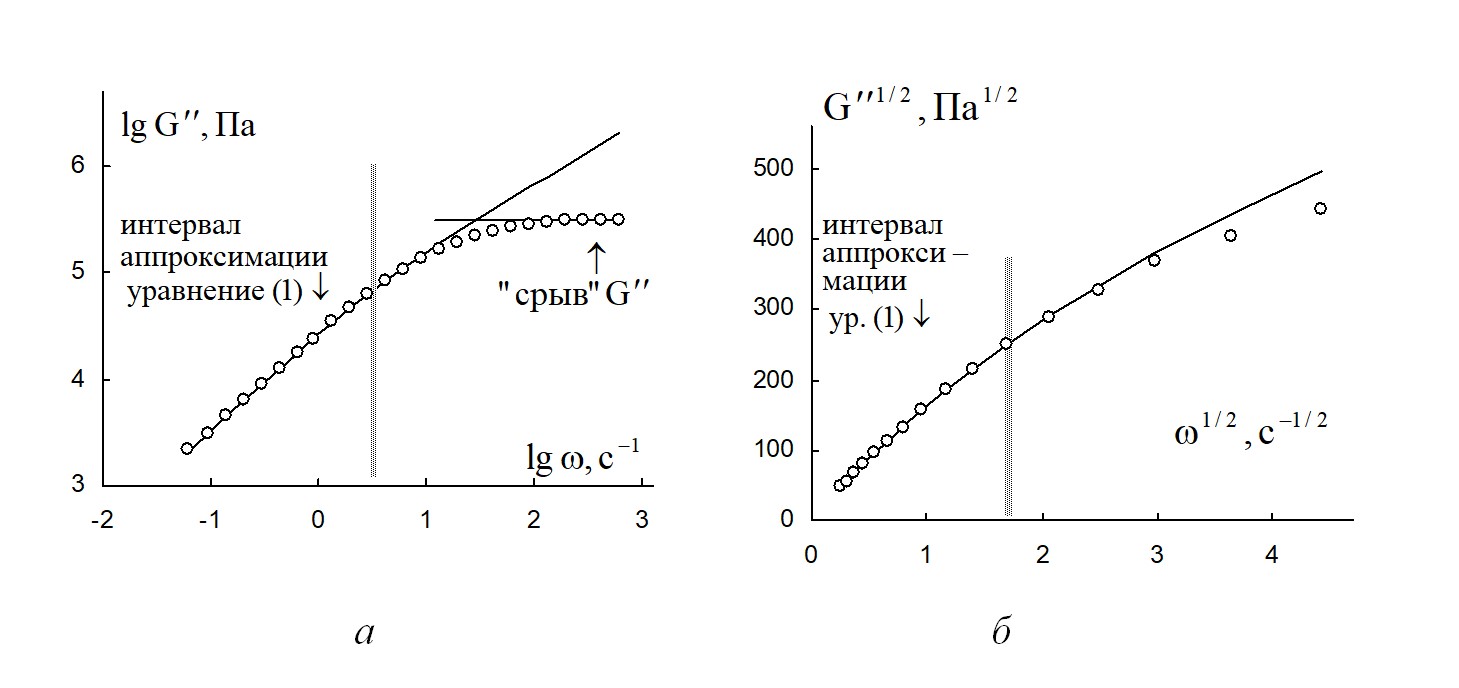
Рисунок 2 - Зависимость модуля потерь расплава полимера поли(ε-капролактан) от циклической частоты при температуре 70 ºС
Примечание: а – в двойных логарифмических координатах; б – в корневых координатах на интервале до 20 с-1
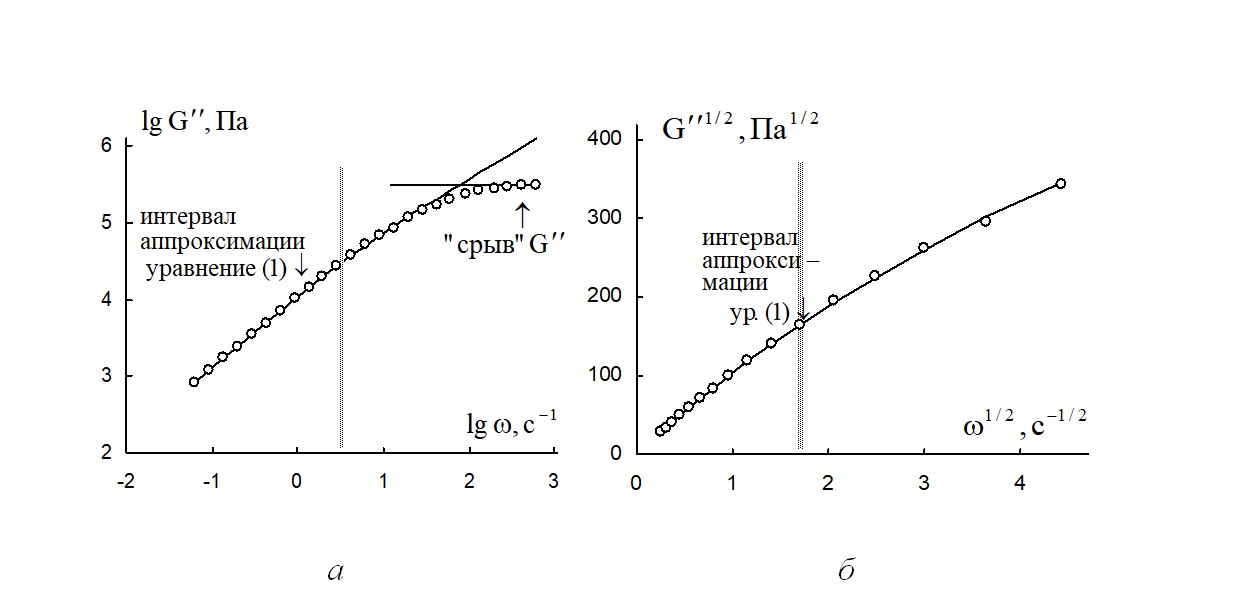
Рисунок 3 - Зависимость модуля потерь расплава полимера поли(ε-капролактан) от циклической частоты при температуре 100 ºС
Примечание: а – в двойных логарифмических координатах; б – в корневых координатах до 20 с-1
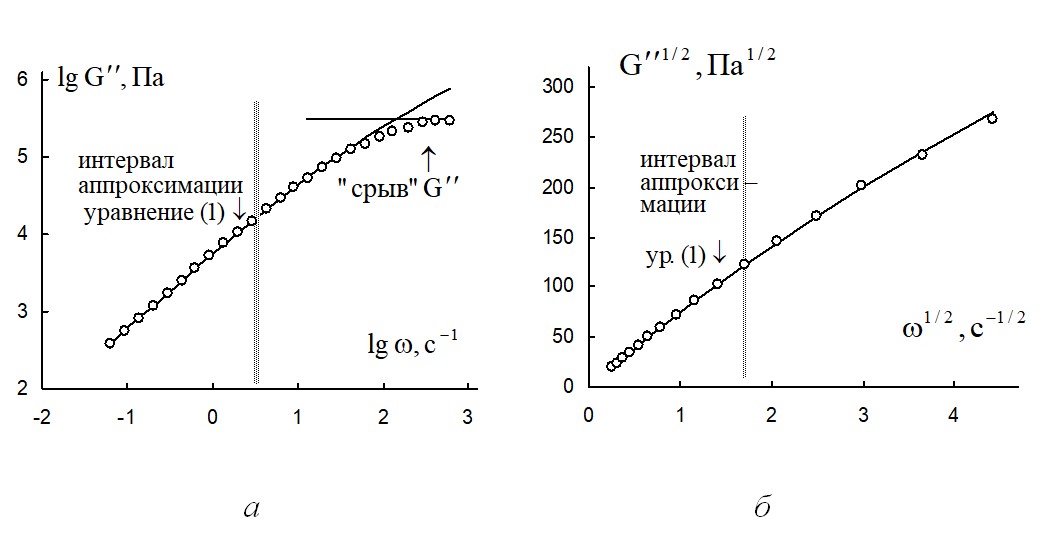
Рисунок 4 - Зависимость модуля потерь расплава полимера поли(ε-капролактан) от циклической частоты при температуре 130 ºС
Примечание: а – в двойных логарифмических координатах; б – в корневых координатах до 20 с-1
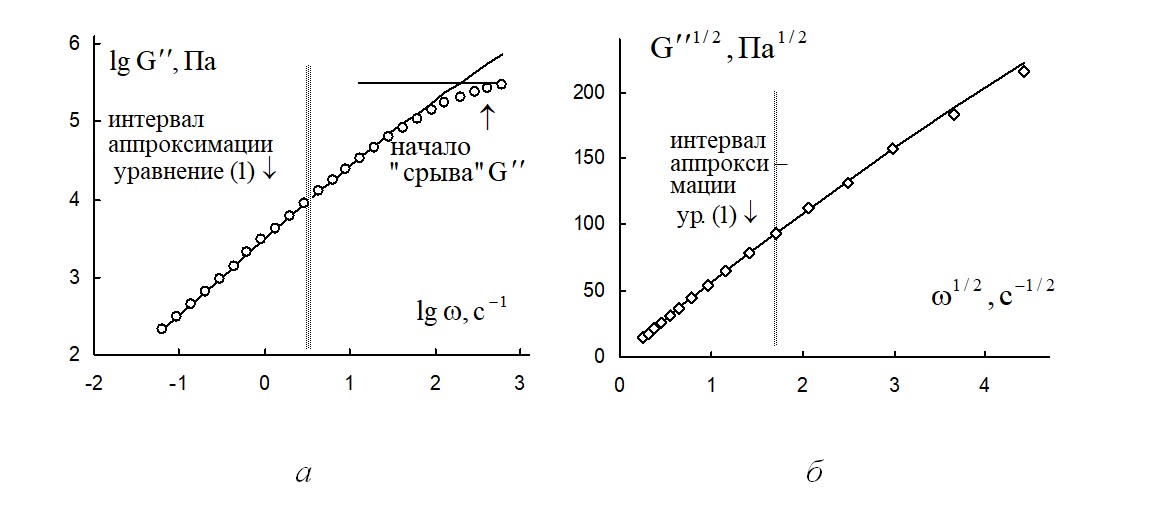
Рисунок 5 - Зависимость модуля потерь расплава полимера поли(ε-капролактан) от циклической частоты при температуре 160 ºС
Примечание: а – в двойных логарифмических координатах; б – в корневых координатах до 20 с-1
Таблица 1 - Коэффициенты уравнения (1) для модуля потерь в расплаве полимера поли(ε-капролактан) при различных температурах
Уравнение для модуля накопления в случае разрыва зацеплений имеет вид :
Поскольку то уравнение для динамической упругости
приобретает вид
Первое слагаемое представляет собой структурную часть модуля накопления (или динамической упругости), обусловленную упругостью ассоциатов макромолекул; второе слагаемое описывает часть модуля накопления (или динамической упругости), связанную с упругостью отдельных макромолекул.
Таким образом, макромолекулы и их «упругие» ассоциаты можно представить в виде некоторых «молекулярных пружин». С увеличением частоты колебаний и, соответственно, скорости сдвига ωγ0 зацепления разрываются, и упругость «молекулярных пружин» уменьшается. Соответственно, с ростом частоты уменьшается величина динамической упругости и увеличивается величина G'.
Если агрегаты (или ассоциаты макромолекул) отсутствуют, то динамическая упругость обеспечивается упругими свойствами отдельных частиц, т.е. величиной . Используя кинетические уравнения, можно рассчитать значения коэффициентов в уравнении (3):
При низких циклических частотах количество «упругих» ассоциатов и зацеплений может увеличиваться с ростом частоты, поскольку возникают дополнительные упругие контакты при столкновениях макромолекул. Поэтому при низких частотах может наблюдаться участок, описываемый уравнением, линейным в корневых координатах, а именно:
При дальнейшем уменьшении частоты колебаний в отдельных случаях появляется кривая степенной зависимости G' = g2ωn, где n ≈ 2.
С помощью кинетических уравнений можно получить значения коэффициентов:
Коэффициент ΔG'1/2 является положительным, если k''0 > k''2, и отрицательным, если k"0 < k"2. Кривые частотной зависимости модуля накопления (рис. 6–15) можно разделить на отдельные части, которые описываются различными реологическими уравнениями. Пунктирной линией показана возможная степенная зависимость при очень низких частотах.
Выбор интервалов аппроксимации можно осуществить, используя корневые координаты, как показано на рис. 7. Прямолинейные зависимости указывают на возможность применения уравнения (5). Экспериментальная зависимость, постепенно выходящая на «прямую» в области высоких частот, указывает на возможность применения уравнения (3).
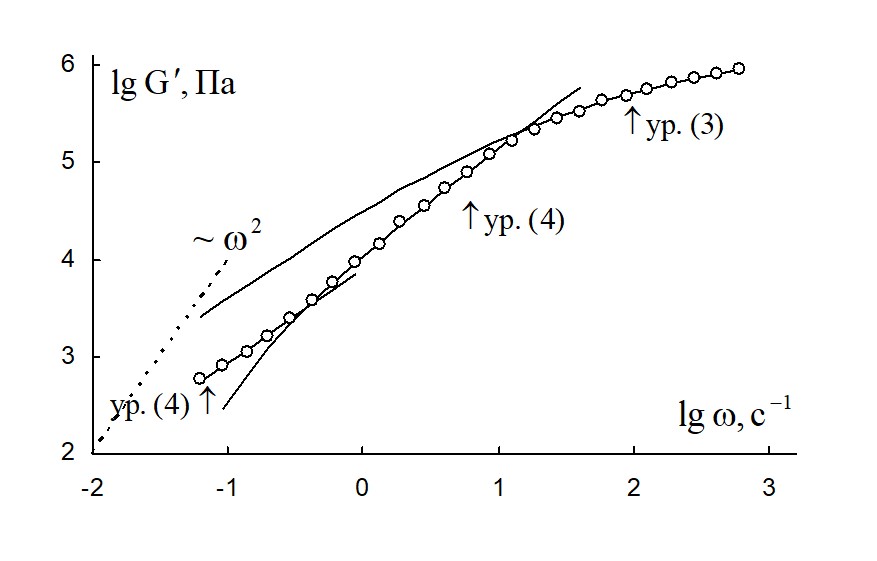
Рисунок 6 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты при температуре 62 ºС в двойных логарифмических координатах
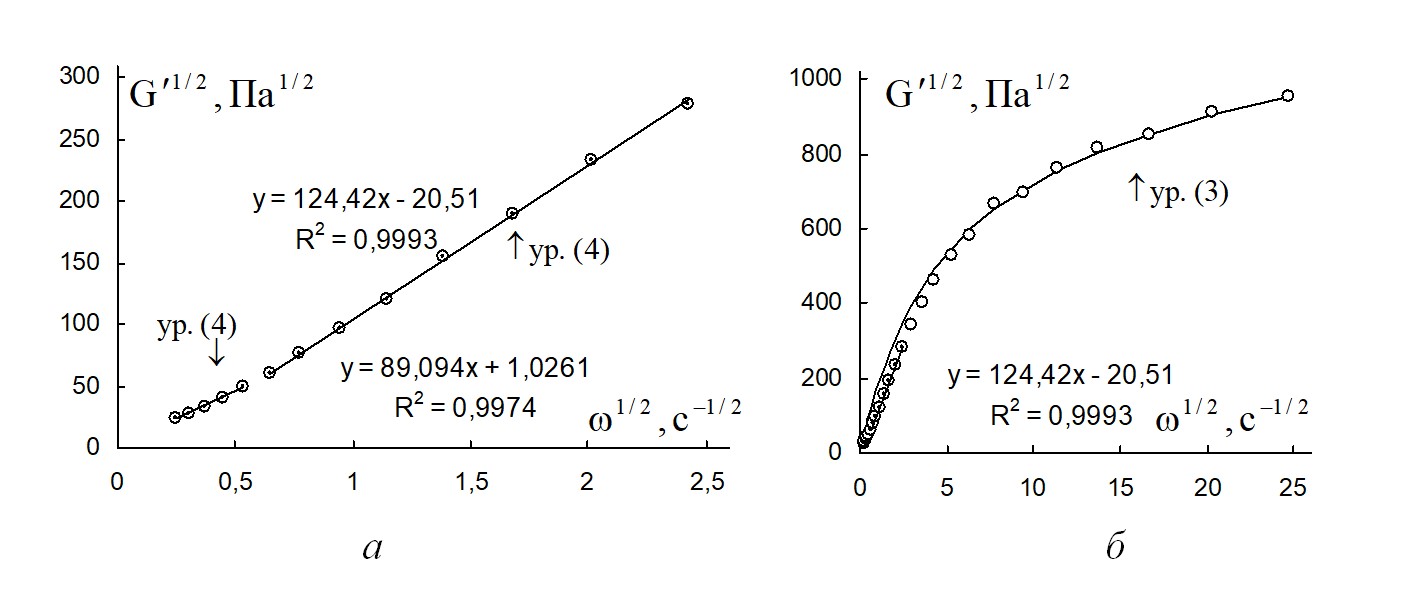
Рисунок 7 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты в корневых координатах при температуре 62 ºС
Примечание: а – на интервале низких частот; б – на полном интервале частот
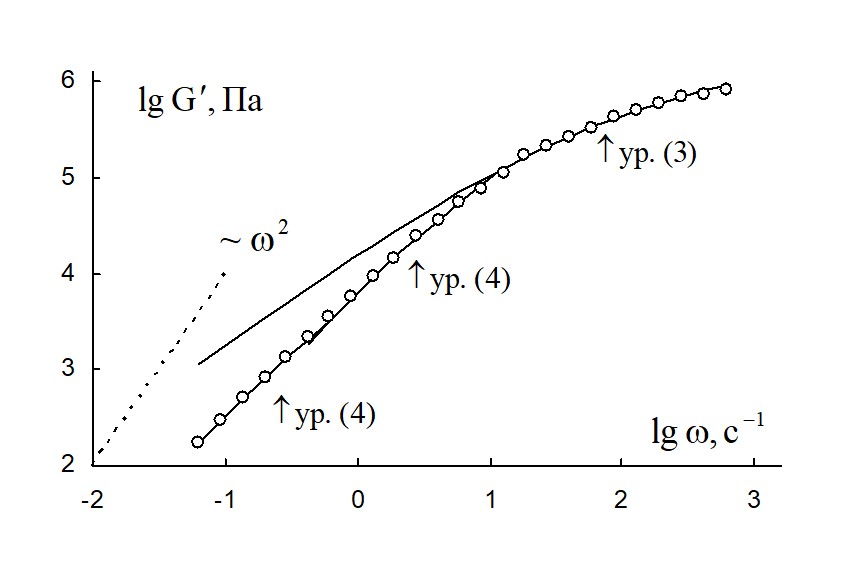
Рисунок 8 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты при температуре 70 ºС в двойных логарифмических координатах
При достижении высоких температур (130 ºС и 160 ºС) в районе низких частот появляется степенная зависимость модуля накопления, близкая к квадратичной (рис. 12, 14):
где:
n = 1,63 и g''00 = 24,5 при 130 ºС;
n = 1,84 и g''00 = 15,7 при 160 ºС.
Коэффициенты реологических уравнений (3) и (5) представлены в таблице 2.
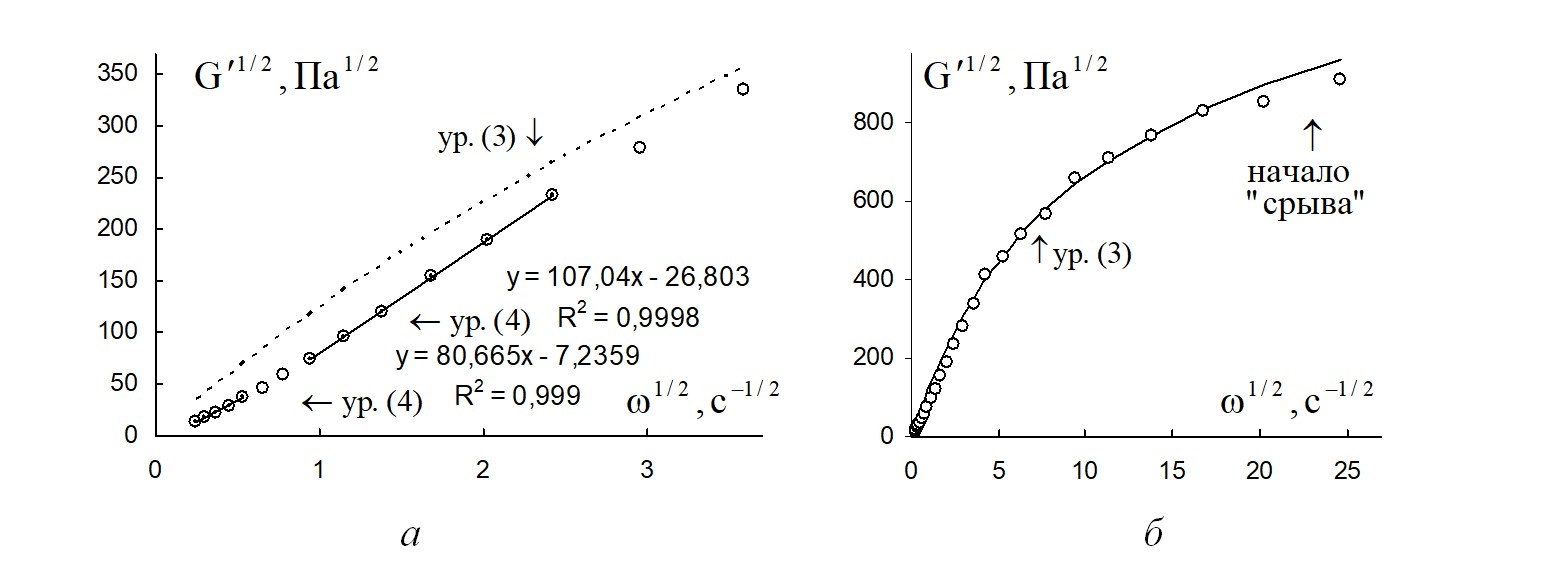
Рисунок 9 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты в корневых координатах при температуре 70 ºС
Примечание: а – на интервале низких частот; б – на полном интервале частот
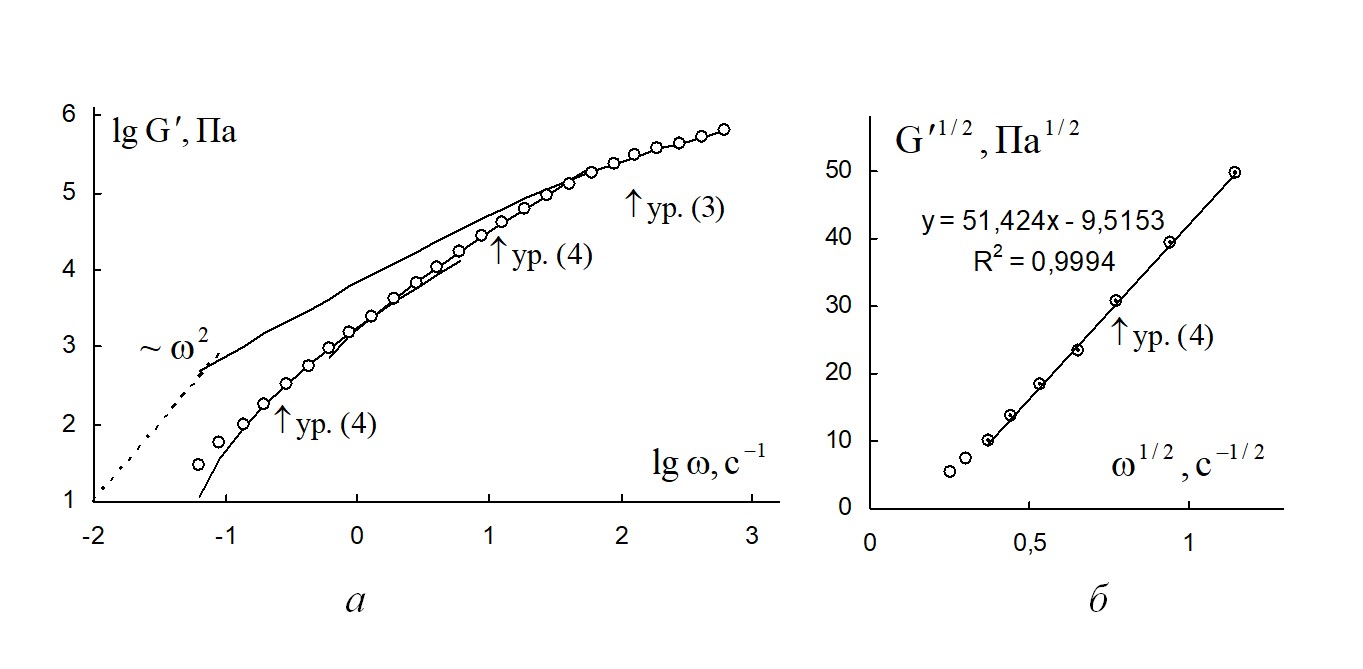
Рисунок 10 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты при температуре 100 ºС
Примечание: а – в двойных логарифмических координатах на полном интервале частот; б – в корневых координатах на интервале частот ниже 2 с-1
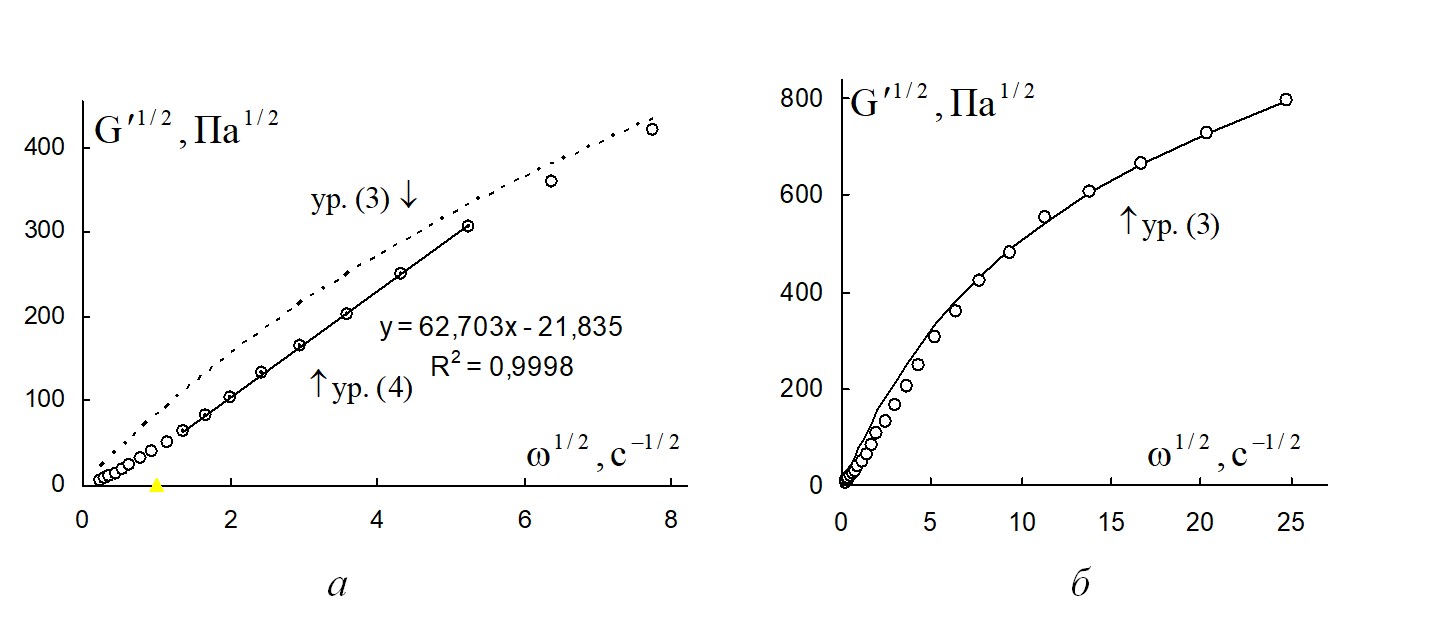
Рисунок 11 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты в корневых координатах при температуре 100 ºС
Примечание: а – на интервале частот ниже 60 с-1; б – на полном интервале частот
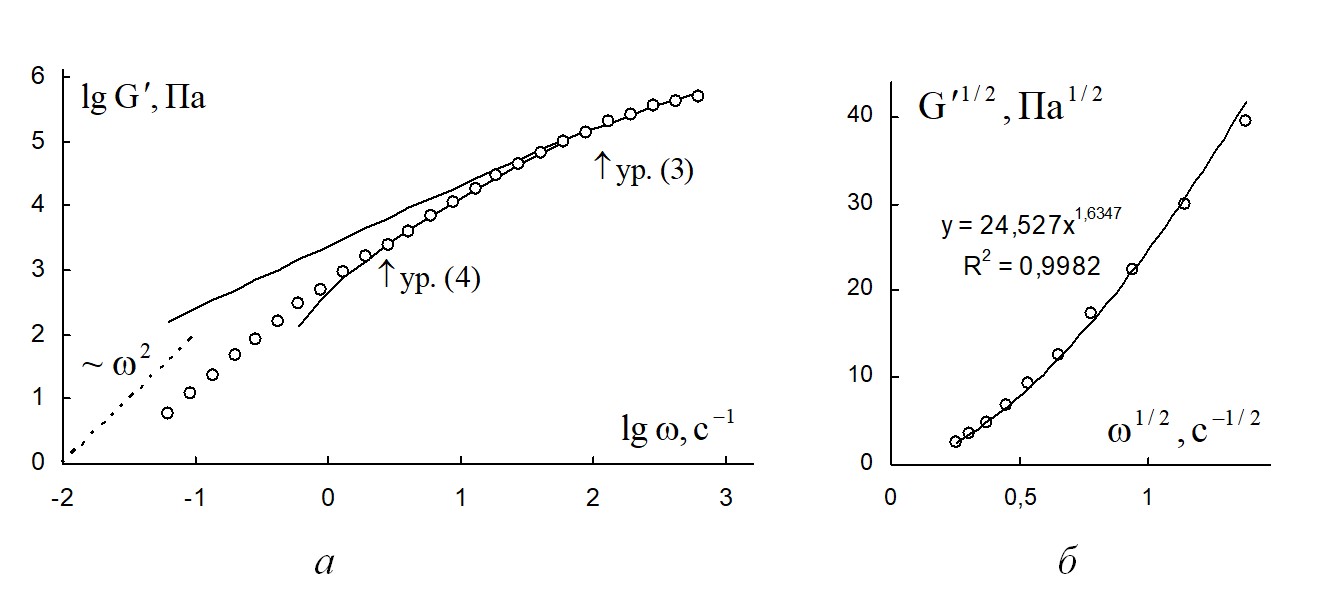
Рисунок 12 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты при температуре 130 ºС
Примечание: а – в двойных логарифмических координатах на полном интервале частот; б – в корневых координатах на интервале частот ниже 3 с-1
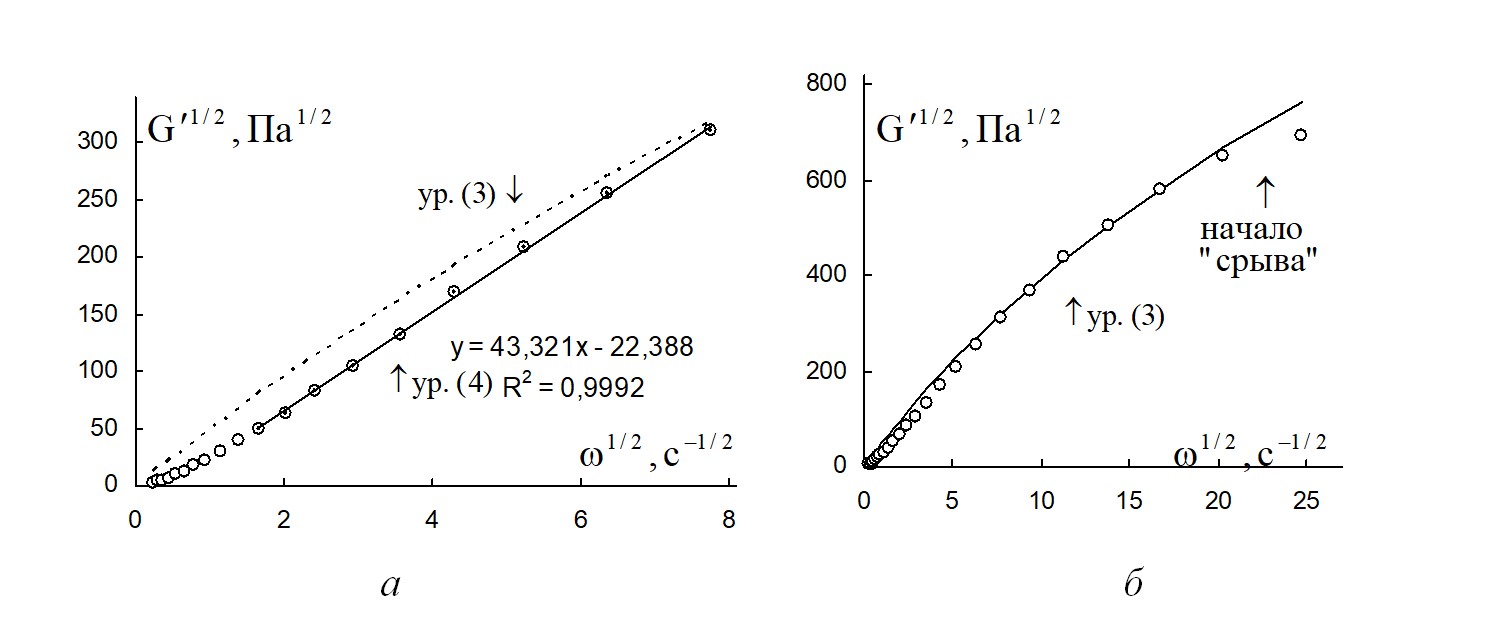
Рисунок 13 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты в корневых координатах при температуре 130 ºС
Примечание: а – на интервале частот ниже 60 с-1; б – на полном интервале частот
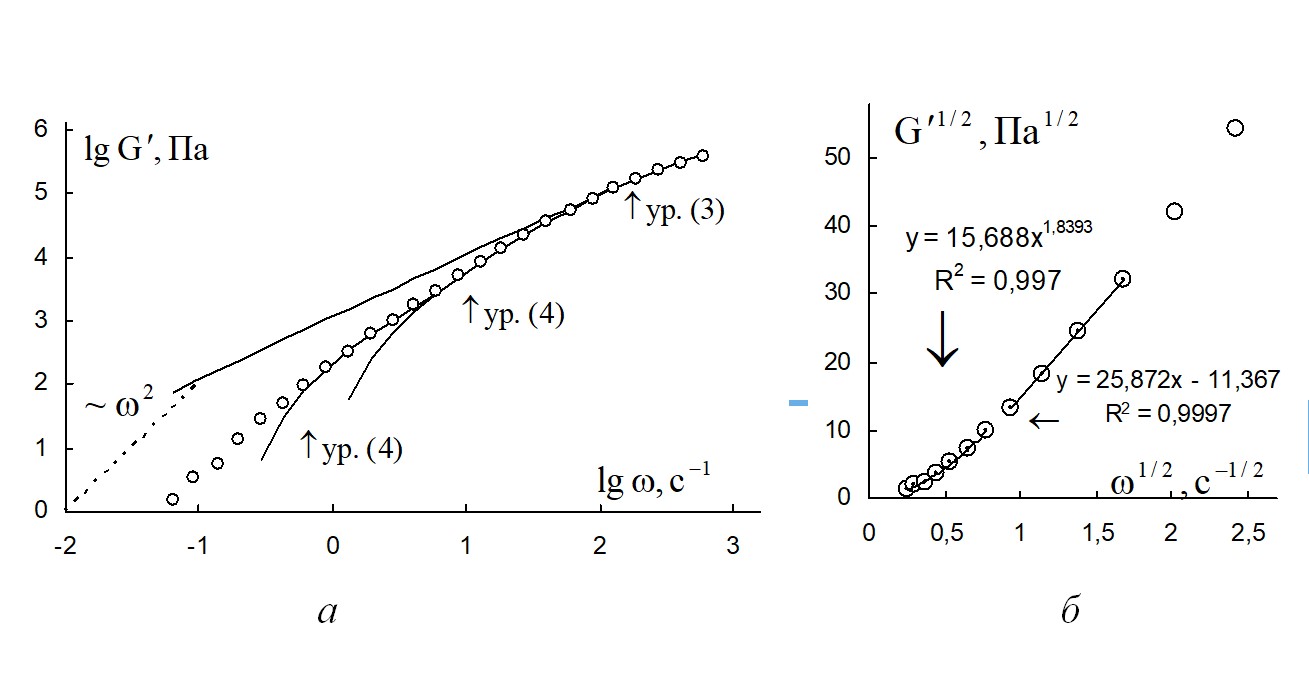
Рисунок 14 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты при температуре 160 ºС
Примечание: а – в двойных логарифмических координатах на полном интервале частот; б – в корневых координатах на интервале частот ниже 6 с-1
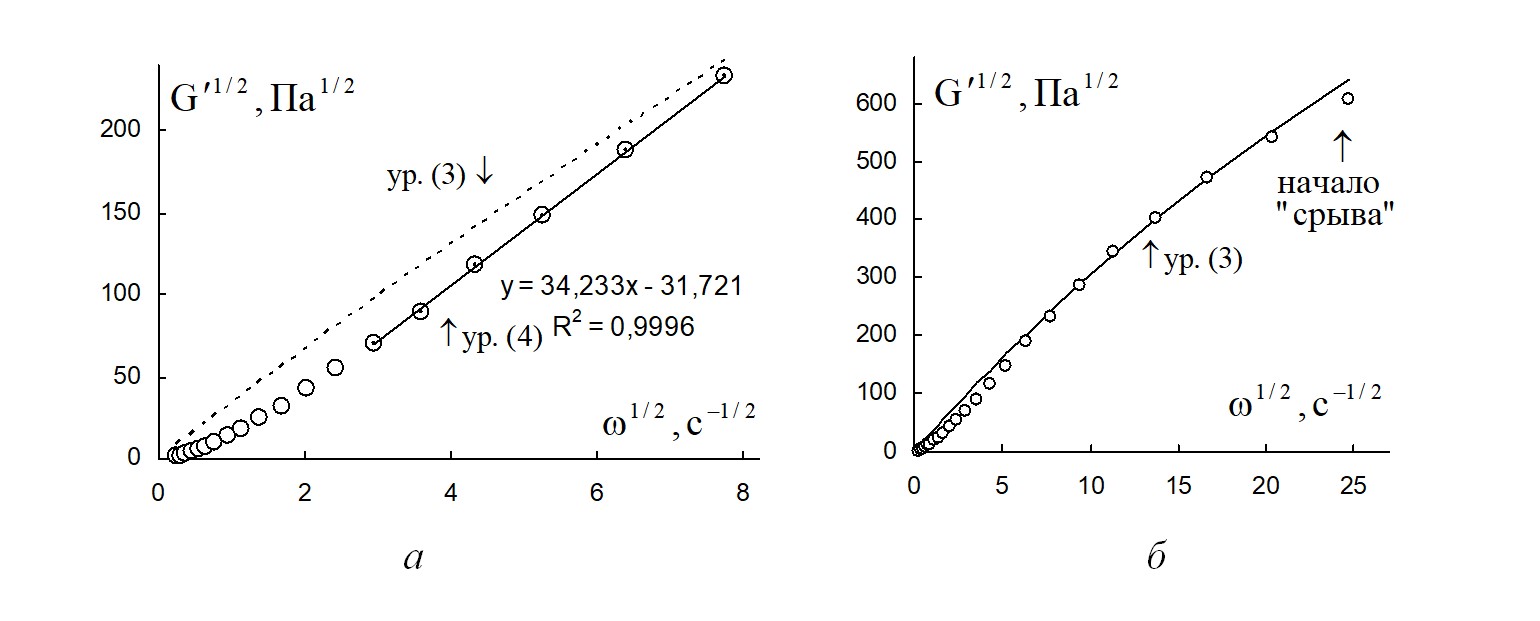
Рисунок 15 - Зависимость модуля накопления расплава полимера поли(ε-капролактан) от циклической частоты в корневых координатах при температуре 160 ºС
Примечание: а – на интервале частот ниже 60 с-1; б – на полном интервале частот
Таблица 2 - Коэффициенты уравнения модуля накопления для расплава полимера поли(ε-капролактан) при различных температурах
Судя по табл. 2, при самой высокой температуре 160 ºС «упругое» поведение резко изменяется. Величина коэффициента g'' резко увеличивается, а вклад в упругость отдельных макромолекул практически исчезает
На рис. 15а показаны зависимости коэффициентов компактности χ' и χ" от обратной абсолютной температуры. Экспоненциальные зависимости этих коэффициентов от обратной абсолютной температуры указывают на механизм упругости, связанный с некоторой энергией активации.
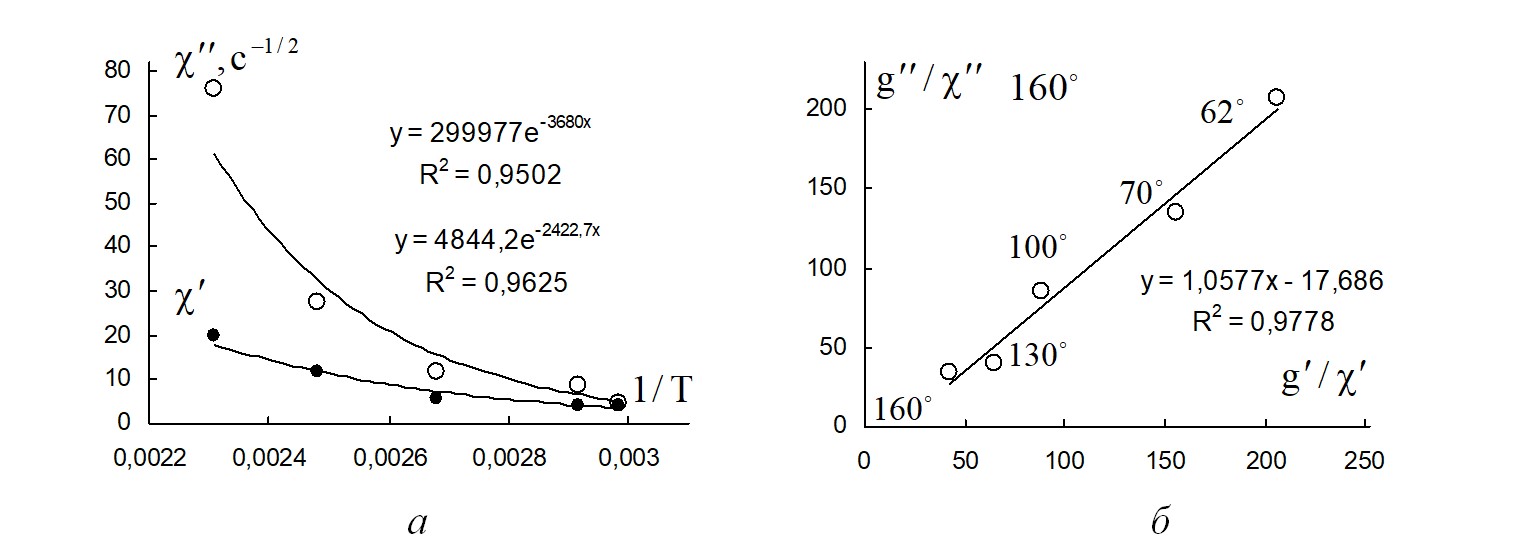
Рисунок 16 - Зависимости коэффициентов реологических уравнений, полученных для расплава полимера поли(ε-капролактан)
Примечание: а – зависимость коэффициентов компактности от обратной температуры; б – взаимозависимость структурной части динамической упругости и структурной части динамической вязкости
Корреляция между этими величинами указывает на прямую связь между упругими свойствами и вязкими свойствами полимерного расплава при сдвиговых осцилляциях. Описанная корреляция между «вязкими» и «упругими» коэффициентами объясняется структурной природой вязких и упругих свойств расплава полимера.
На интервале низких частот можно сопоставить соответствующие характеристики для вязкой составляющей и упругой составляющей при различных температурах. Коэффициенты закономерно изменяются при изменении температуры (табл. 2).
Небольшое увеличение положительной величины ΔG'1/2 с ростом температуры может быть связано с увеличением величины коэффициента k''0. Коэффициент k''0 пропорционален вероятности спонтанного разрыва зацеплений и, потому должен увеличиваться с ростом температуры.
Сравним абсолютную величину коэффициентов ΔG'1/2 и g''0 в виде отношения: .
Если справедливо неравенство то
что и подтверждается данными в таблице 2.
При высоких скоростях сдвига в некоторых случаях наблюдается , «срыв течения» или «срыв динамических модулей», что выражается в резком снижении величин G'' или G' вплоть до постоянной величины, не зависящей от скорости сдвига или частоты колебаний. Это явление представлено на рис. 1–5 в этой статье. Мы предполагаем, что явление «срыва» при осциллирующем течении связано со сдвиговым расслоением, т.е. с переходом от гомогенного течения в образце расплава к негомогенному течению, где возникают слои с разными вязкими свойствами и разной структурой. Возможно, что переход происходит при достижении некоторой предельной энергии, независимо от температуры расплава.
Действительно, энергия, запасенная за первую четверть периода за счет внешних сил, равна Энергия, потерянная за счет вязкости за четверть периода, равна
Таким образом «срыв» величины G'' соответствует достижению некоторой постоянной величины диссипации энергии
Как понятно из вышесказанного, представленная нами реологическая модель является альтернативной по отношению к моделям, использующим механические элементы пружины и демпфера и тем самым объединяющим вязкость и упругость в одном математическом выражении. Отметим далее некоторые другие подходы, использованные для описания вязкоупругости .
Например, в работе динамические модули описывают простыми эмпирическими соотношениями G'' = K"ωn" и G' = K'ωn' , что соответствует экспериментальным данным на небольших интервалах измерений. Среди моделей, объединяющих вязкость и упругость, можно выделить модель Фридриха-Брауна , , в которой используются всего по семь подгоночных параметров для G'' и G'.
4. Заключение
Рассмотрены вязкоупругие свойства расплава полимера поли(ε-капролактан) — алифатический полиэфир. Обнаружено, что упругие и вязкие свойства существенно отличаются по характеру реологических кривых. В то же время имеется некоторая корреляция между коэффициентами реологических уравнений, описывающих вязкое и упругое поведение.
Изменение коэффициентов реологических уравнений с температурой соответствует выводам структурной реологической модели.
Явление «срыва» осциллирующего течения проявляется в «срыве» величины модуля потерь G", т.е. выходе значения модуля потерь на «плато» с постоянной величиной G"SP, которая практически не зависит от температуры расплава данного полимера.
