Расчет гомологических серий химических соединений систем {Li+ - Fe2+ - (PO4)3-, (La3+ - Sr2+ - Ti4+ - O2-), (Bi3+ - Sr2+ - Ca2+ - Cu2+ - O2-)

Известно, что любое химическое соединение (ХС) является членом гомологической серии (ГС) с n ≥ 1. Гомологическим сериям ХС характерна важная особенность: фундаментальные свойства ее членов изменяются закономерно

Так, опубликованы формулы ГС, полученных на основе (только!) экспериментов для некоторых систем химических элементов (ХЭ): для систем (Mo – O), (W – O), (Ti – O), (V – O)

Однако в случае, например, «фаз Магнели» все опубликованные в

Аналогично, учитывая необходимость электро нейтральности формул ХС, ГС для системы (La – Ni – O)

LanNinO3n – 1

Кроме этого, ГС для системы (Y – Ba – Cu – O) следует считать не четырех-, а пяти компонентной: Y2Ba4Cu6 + nO14 + n

Из-за отсутствия знаний закона формирования ГС обобщения полученных в работах

Авторы работы

TlmBa2Can - 1CunO2(n + 1)m (m = 1, 2; n = 1, 2, 3)

Согласно авторам для системы (Bi3+ – Sr2+ – Ca2+ – Cu2+ – O2-)

В работах

Используя разработанный в работах

Цель работы: разработать упрощенный способ расчета формул ГС на основе заданного (базового) ХС (ХСn(bas)).

В работе задача решается в обобщенном варианте. По этой причине, когда в написании уравнения реакции не используются концентрации реагентов, вместо знака равенства используется стрелка, которая указывает на направление взаимодействия. Все составы кластеров при необходимости определяются составом конкретного базового кластера (ХСn(bas)). Искомые формулы кластеров всех приводимых в работе реакций выделяются жирным шрифтом. Схема определения состава заряженных кластеров (ЗК), которые состоят только из катионов, описана в работах

(1)

(2)

(3)

где (0 < t, r, w, v), четырех компонентное ХС (ЧХС), пятикомпонентное ХС (ПХС).

Формирование ГС независимо от сложности системы ионов ХЭ происходит по схеме:

(4)

Формула ГС в обобщенном виде выглядит так:

(5)

Для того чтобы определить формулу ГС, необходимо рассчитать формулы ХСn = 1 и ∆ в зависимости от формулы ХСn(bas):

(6)

(7)

Чтобы определить величину k, которая связана с положением базового кластера в его ГС, нужно пройти в обратном направлении схему формирования ГС (4) в направлении от ХСn(bas) и ЗКn(bas) к кластерам ХСn = 1 и ЗКn = 1:

(8)

Однако, для определения k можно использовать более простую схему:

(9)

Так как n > 0, то в данном случае {(n(bas) – k) > 0} и n(bas) > k. Анализ для систем любой сложности свойственна следующая зависимость:

(10)

Тогда, учитывая зависимость (7), формула ветви ХС гомологической серии будет выглядеть так:

(11)

3.1. Система (Aa+ – Bb+ – Cc–) ≡ {Li+ – Fe2+ – (PO4)3-}. Направление BcCb ≡ Fe2O3

Пусть базовым кластером будет (Li+12Fe2+15(PO4)3-14

В сиситеме {Li+ – Fe2+ – (PO4)3-} кластеры в виде т. 1 и т. 2 образуются согласно

(12)

(13)

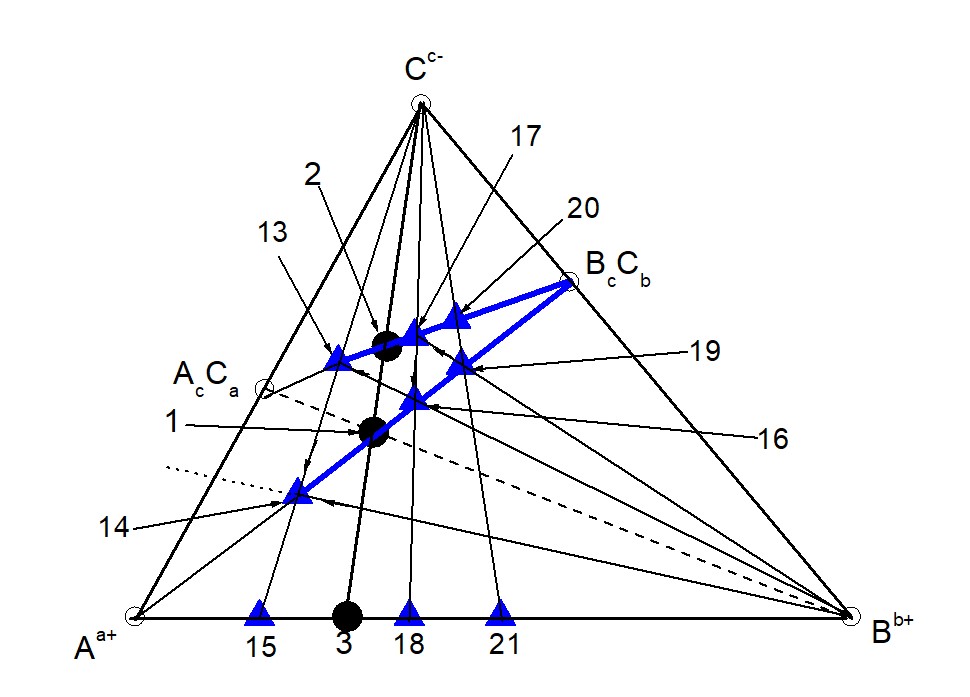
Рисунок 1 - Система (Aa+ - Bb+ - Cc-) ≡ {Li+ - Fe2+ - (PO4)3-} – βm-ГС

DOI:10.60797/CHEM.2025.5.2.1

На рисунке 1:

т. 1 = [Li6Fe3(PO4)2]6+; т. 2 = Li12Fe6(PO4)8;

т. 3 = [Li6Fe3]12+; т. 13 = Li12Fe3(PO4)6;

т. 14 = [Li12Fe3(PO4)2]12+; т. 15 = [Li12Fe3]18+;

т. 16 = [Li12Fe9(PO4)6]12+; т. 17 = Li12Fe9(PO4)10;

т. 18 = [Li12Fe9]30+; т. 19 = ТЗКn(bas) = [Li12Fe15(PO4)10]12+;

т. 20 = ТХСn(bas) = Li12Fe15(PO4)14.

Формула (ТЗКn(bas) = т. 19), ТЗКn(bas) + 1 и ТХСn(bas) + 1 определятся так:

(14)

(15)

(16)

Согласно (5) получим формулу ∆:

(17)

Для того чтобы определить формулу ТХСn = 1, необходимо из формулы ТХСn(bas) вычесть ∆ максимальное количество раз при условии сохранения Fe2+ в получаемой таким образом формуле ТХС. Как видно, чтобы избежать потерю Fe2+ в формуле ТХС, из формул (ТХСn(bas) = т. 20 = Li12Fe15(PO4)14) и (ТЗКn(bas) = т. 19 = [Li12Fe15(PO4)10]12+) можно вычесть (∆ = Fe6(PO4)4) только 2 раза, что соответствует k = 2 и n(bas) = k + 1 = 3. В результате получим: (ТХСn = 1 = т. 13 = Li12Fe3(PO4)6) и (ТЗКn = 1 = т. 14 = [Li12Fe3(PO4)2]12+). При этом, следует обратить внимание на то, что в формуле (ТХС = т. 2 = Li12Fe6(PO4)8 ≡ 4Li3(PO4) + + 2Fe3(PO4)2) соотношение (Li3(PO4)/Fe3(PO4)2 = 2), а в формуле (ТХСn = 1 = т. 13 = Li12Fe3(PO4)6 ≡ 4Li3(PO4) + Fe3(PO4)2) соотношение (Li3(PO4)/ Fe3(PO4)2 = 4).

Следовательно, (ТХСn = 1 = т. 13 = Li12Fe3(PO4)6) находится на отрезке (т. 2 – Li3(PO4)), а {ТЗКn = 1 = т. 14 = [Li12Fe3(PO4)2} — на отрезке (т. 1 – Li+). Важно также отметить, что продолжение отрезка {Fe2+ - (ТЗКn = 1 = т. 14 = [Li12Fe3(PO4)2]12+)} не пересекается с отрезком {Li3(PO4 – Fe3(PO4)2}указывая тем самым на отсутствия ТХС, который бы следовал за (ТХС = т. 13) в сторону Fe3(PO4)2. Сказанное графически подтверждает, что (ТЗК = т. 14) и (ТХС = т. 13) является первыми членами в ГС, третьим гомологом которой является (ТХСn(bas) = т. 20 = Li12Fe15(PO4)14).

(18)

3.2. Система (Aa+ – Bb+ – Dd+ – Cc–) ≡ (La3+ – Sr2+ – Ti4+ – O2-)

Рассмотрим расчет ГС на примере системы (La3+ – Sr2+ – Ti4+ – O2-). Тогда Aa+ ≡ La3+, Bb+ ≡ Sr2+, Dd+ ≡ Ti4+, Cc- ≡ O2-, AcCa ≡ La2O3, BcCb ≡ SrO, DcCd ≡ TiO2.

Пусть базовым кластером будет (La3+2Sr2+4Ti4+6O2-19 [38] = ЧХСn(bas) = AtbdcBradcDwabcC(t + r + w)abd = т. 1) — рис. 2, 3.

Формулы кластеров, которые характеризуют систему (Aa+ – Bb+ – Dd+ – Cc–) ≡ (La3+ – Sr2+ – – Ti4+ – O2-) определятся следующим образом:

(19)

(20)

(21)

(22)

(23)

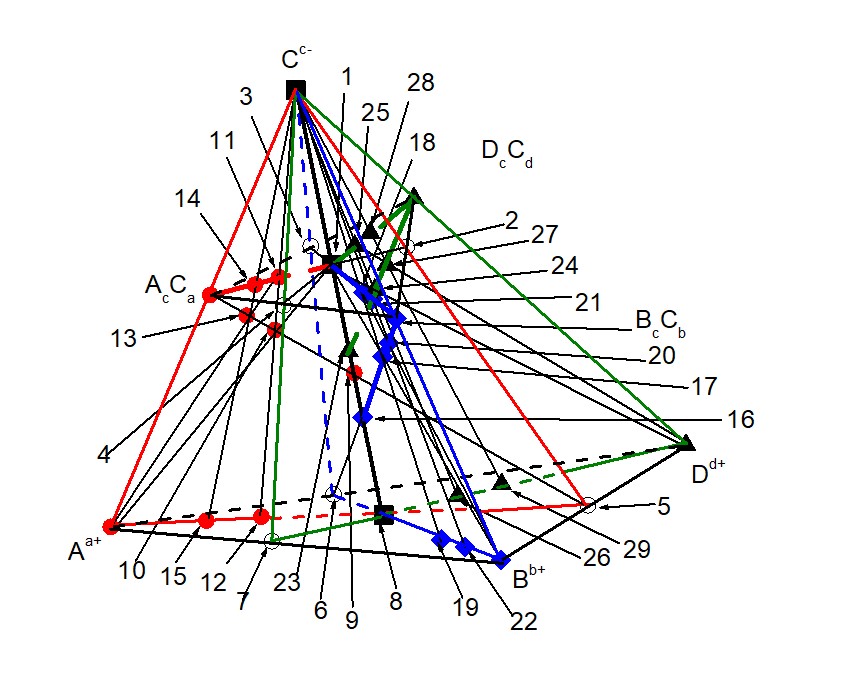
Рисунок 2 - Система (Aa+ – Bb+ – Dd+ – Cc–) ≡ (La3+ – Sr2+ – Ti4+ – O2-)

DOI:10.60797/CHEM.2025.5.2.2

На рисунке 2:

т. 1 = ЧХСn(bas) = La3+2Sr2+4Ti4+6O2-19 ≡ La6Sr12Ti18O57;

т. 2 = Sr4Ti6O16; т. 3 = La2Ti6O15;

т. 4 = La2Sr4O7; т. 5 = [Sr12Ti18]96+;

т. 6 = [La2Ti6]30+; т. 7 = [La2Sr4]14+;

т. 8 = [La2Sr4Ti6]38+; т. 9 = ЧЗКn(bas) = [La6Sr12Ti18O9]96+;

т. 10 = [La38Sr12Ti18O57]96+; т. 11 = La38Sr12Ti18O105;

т. 12 = [La38Sr12Ti18]210+; т. 13 = [La70Sr12Ti18O105]63+;

т. 14 = La70Sr12Ti18O153; т. 15 = [La70Sr12Ti18]306+;

т. 16 = ЧЗКn(bas) = [La2Sr4Ti6O4]30+; т. 17 = [La2Sr19Ti6O19]30+;

т. 18 = La6Sr27Ti18O72; т. 19 = [La6Sr27Ti18]144+;

т. 20 = [La6Sr27Ti18O27]90+; т. 21 = La6Sr42Ti18O87;

т. 22 = [La6Sr42Ti18]174+; т. 23 = ЧЗКn(bas) = [La4Sr8Ti12O24]28+;

т. 24 = [La4Sr8Ti19O38]28+; т. 25 = La4Sr8Ti19O52;

т. 26 = [La4Sr8Ti19]104+; т. 27 = [La4Sr8Ti26O52]28+;

т. 28 = La4Sr8Ti26O66; т. 29 = [La4Sr8Ti26]132+;

т. 30 = La32Sr12Ti18O48]96+; т. 31 = La32Sr12Ti18O96;

т. 32 = [La32Sr12Ti18]192+; т. 35 = [La2Sr15Ti6]60+.

3.2.1. Подсистема (Bb+ – т. 6 – О2–) ≡ (Sr2+ - [La2Ti6]30+ - О2–). Направление BcCb ≡ SrO

Для того чтобы рассчитать формулу ГС, которой принадлежит (ЧХСn(bas) = т. 1 = La3+2Sr2+4Ti4+6O2-19), в подсистеме (Bb+ – т. 6 – Cc–) ≡ (Sr2+ – т. 6 – O2-) нужно определить значение ∆, n(bas) и рассчитать формулы ЧЗКn(bas), ЧЗКn(bas) + 1 и ЧХСn(bas) + 1 следующим образом:

(24)

(25)

(26)

Рисунок 3 - Подсистема (Bb+ – т. 6 – Cc–) ≡ (Sr2+ - [La2Ti6]30+ - О2–). Направление BcCb ≡ SrO

DOI:10.60797/CHEM.2025.5.2.3

На рисунке 3:

т. 1 = ЧХСn(bas) = La3+2Sr2+4Ti4+6O2-19 = La6Sr12Ti18O57;

т. 3 = La2Ti6O15; т. 6 = [La2Ti6]30+; т. 8 = [La2Sr4Ti6]38+;

т. 16 = ЧЗКn(bas) =[La6Sr12Ti18O12]90+; т. 17 = [La6Sr27Ti18O27]90+;

т. 18 = La6Sr27Ti18O72; т. 19 = [La6Sr27Ti18]144+;

т. 20 = [La6Sr27Ti18O27]90; т. 21 = La6Sr42Ti18O87;

т. 22 = [La6Sr42Ti18]174+; т. 33 = [La2Sr15Ti6O15]30+;

т. 34 = La2Sr15Ti6O30; т. 35 = [La2Sr15Ti6]60+.

Согласно (6) получим формулу ∆:

(27)

(28)

Для того чтобы определить формулу ЧХСn = 1, необходимо из формулы ЧХСn(bas) вычесть ∆ максимальное количество раз при условии сохранения Sr2+ в получаемой таким образом формуле ТХС. Как видно, из формул (ЧХСn(bas) = т. 1 = La2Sr4Ti6O19) нельзя вычитать (∆ = Sr15O15), что соответствует k = 0 и n(bas) = 1. В результате подтвердится, что: ЧХСn = 1 = т. 1 = La2Sr4Ti6O19) и (ЧЗКn = 1 = т. 16 = [La2Sr4Ti6O4]30+). При этом, следует обратить внимание на то, что в формуле (т. 34 = La2Sr15Ti6O30 = 15SrO + La2Ti6O15) соотношение SrO/ La2Ti6O15 = 15/1, а в формуле (ЧХСn = 1 = т. 1 = La2Sr4Ti6O19) соотношение (SrO/La2Ti6O15 = 4/1). Следовательно, (ЧХСn = 1 = т. 1 = La2Sr4Ti6O19) находится на отрезке (т. 3 – т. 34), а {ЧЗКn = 1 = т. 16 = [La2Sr4Ti6O4]30+} – на отрезке (т. 6 – 33), где:

(29)

(30)

Важно также отметить, что продолжение отрезка {Sr2+ - (ТЗКn = 1 = т. 16 = [La2Sr4Ti6O4]30+)} не пересекается с отрезком (SrO – т. 3) указывая тем самым на отсутствия ТХС, который бы следовал за (ТХС = т. 1) в сторону (La2Ti6O15 = т. 3). Сказанное графически подтверждает, что (ТЗКn(bas) = 1 = т. 16) и (ТХСn(bas) = 1 = т. 1) являются первыми членами в ГС. Тогда в соответствии с(11) получим:

(31)

3.3. Cистема (Aa+- Bb+- Dd+- Ff+- Cc–) ≡ (Bi3+- Sr2+- Ca2+- Cu2+- O2-). Подсистема (Bb+-Dd+- [AtfFva](t + v)af+- Сс–) ≡ (Sr2+- Ca2+- [Bi3+2Cu2+3]12+- O2-)

Рассчитаем формулу ГС на примере системы (Bi3+-Sr2+-Ca2+-Cu2+-O2-). Тогда Aa+ ≡ Bi3+, Bb+ ≡ Sr2+, Dd+ ≡ Ca2+, Ff+ ≡ Cu2+, Cc- ≡ O2-, AcCa ≡ Bi2O3, BcCb ≡ SrO, DcCd ≡ CaO, FcCf ≡ CuO. Для конкретизации подсистем (Bb+-Dd+-[AtfFva](t + v)af+-Сс–) и {([AtdfDwafFvad](t+ w + v)adf+ = т. 5)- Bb+-Сс–} рассчитаем формулы кластеров в виде т. 2, т. 3, т. 5, [AtfFva](t + v)af+ и AtfcFvacC( t + v)af применительно к системе (Bi3+-Sr2+-Ca2+-Cu2+-O2-). Пусть базовым кластером будет (Bi2Sr18Ca2Cu3O26 =AtbdfcBradfcDwabfcFvabdc C(t + r + w + v)abdf = ТХСn(bas) = т. 14) – рис. 4, 5.

(32)

(33)

Формулы кластеров в виде [AtfFva](t + v)af+ и AtfcFvacC( t + v)af определятся так:

(34)

(35)

Рисунок 4 - Система (Bb+ - Dd+ - [AtfFva](t + v)af+ - Cc-) ≡ (Bi3+-Sr2+-Ca2+-Cu2+-O2-)

DOI:10.60797/CHEM.2025.5.2.4

На рисунке 4:

т. 1 = Bi2Sr2Ca2Cu3O10; т. 2 = Bi2Ca2Cu3O8; т. 3 = Bi2Sr2Cu3O8;

т.4 = Sr2Ca2O4; т. 5 = [Bi2Ca2Cu3]16+; т. 6 = [Bi2Sr2Cu3]16+;

т. 7 = [Sr2Ca2]8+; т. 8 = [Bi2Sr2Ca2Cu3]20+; т. 9 = [Bi2Sr2Ca2Cu3O2]16+;

т. 10 = [Bi2Sr10Ca2Cu3O10]16+: т. 11 = Bi2Sr10Ca2Cu3O18;

т. 12 = [Bi2Sr10Ca2Cu3]36+; т. 13 = ПХСn(bas) = [Bi2Sr18Ca2Cu3O18]16+;

т. 14 = ПХСn(bas) = Bi2Sr18Ca2Cu3O26; т. 15 = [Bi2Sr18Ca2Cu3]52+;

т. 16 = [Bi2Sr2Ca2Cu3O10]16+; т. 17 = [Bi2Sr2Ca10Cu3O10]16+;

т. 18 = Bi2Sr2Ca10Cu3O18; т. 19 = [Bi2Sr2Ca10Cu3]36+;

т. 20 = [Bi2Sr2Ca18Cu3O18]16+; т. 21 = Bi2Sr2Ca18Cu3O26;

т. 22 = [Bi2Sr2Ca18Cu3]52+; т. 23 = [Bi2Sr8Ca2Cu3O8]16+;

т. 24 = Bi2Sr8Ca2Cu3O16; т. 25 = [Bi2Sr8Ca2Cu3]22+;

т. 26 = [Bi2Sr2Ca8Cu3O8]16+; т. 27 = Bi2Sr2Ca8Cu3O16;

т. 28 = [Bi2Sr2Ca8Cu3]32+.

3.3.1. Подсистема {([AtdfDwafFvad](t + w + v)adf+ = т. 5)- Bb+- Сс–} ≡ [Bi2Ca2Cu3]16+= т. 5) - Sr2+- O2–}. Направление BcCb ≡ SrO

Для того чтобы рассчитать формулу ГС, которой принадлежит (ПХСn(bas) = т. 14), применительно к подсистеме {([AtdfDwafFvad](t + w + v)adf+ = т. 5)-Bb+-Сс–} ≡ ≡ [Bi2Ca2Cu3]16+= т. 5)-Sr2+-O2–} нужно определить значение ∆, n(bas) и рассчитать формулы ПЗКn(bas), ПЗКn(bas) + 1 и ПХСn(bas) + 1 следующим образом:

(36)

(37)

(38)

(39)

(40)

Рисунок 5 - Подсистема {([AtdfDwbfFvbd](t + w + v)bdf+ = т. 5)-Bb+-Сс–}= {[Bi2Ca2Cu3]16+= т. 5)-Sr2+-O2–}

DOI:10.60797/CHEM.2025.5.2.5

На рисунке 5:

т. 1 = La3+2Sr2+4Ti4+6O2-19 ≡ La6Sr12Ti18O57; т. 2 Bi2Ca2Cu3O8; т. 5 = [Bi2Ca2Cu3]16+;

т. 8 = [Bi2Sr2Ca2Cu3]20+; т. 9 = [Bi2Sr2Ca2Cu3O2]16+; т. 10 = [Bi2Sr10Ca2Cu3O10]16+;

т. 11 = La38Sr12Ti18O105; т. 12 = [La38Sr12Ti18]210+; т. 13 = ПЗКn(bas) = [Bi2Sr18Ca2Cu3O18]16+;

т. 14 = ПХСn(bas) = Bi2Sr18Ca2Cu3O26; т. 15 = [La70Sr12Ti18]306+; т. 23 = [Bi2Sr8Ca2Cu3O8]16+;

т. 24 = Bi2Sr8Ca2Cu3O16; т. 25 = [Bi2Sr8Ca2Cu3]22+.

Для того чтобы определить формулу ПХСn = 1, необходимо из формулы ПХСn(bas) вычесть ∆ максимальное количество раз при условии сохранения Sr2+ в получаемой таким образом формуле ПХС. Как видно, из формул (ПХСn(bas) = т. 14 = Bi2Sr18Ca2Cu3O26) можно вычесть (∆ = Sr8O8) только два раза, что соответствует k = 2 и n(bas) = 3. В результате получим: (ПХСn(bas) = 1 = т. 1 = Bi2Sr2Ca2Cu3O10) и (ПЗКn(bas) = 1 = т. 9 = [Bi2Sr2Ca2Cu3O2]16+). При этом, следует обратить внимание на то, что в формуле (т. 24 = Bi2Sr8Ca2Cu3O16) = 8SrO +  Bi2Ca2Cu3O8) соотношение SrO/Bi2Ca2Cu3O8 = 8, а в формуле (ПХСn = 1 = т. 1 = = Bi2Sr2Ca2Cu3O10 = 2SrO + Bi2Ca2Cu3O8) соотношение (SrO/Bi2Ca2Cu3O8 = 2). Следовательно, (ПХСn = 1 = т. 14 = Bi2Sr2Ca2Cu3O10) находится на отрезке (т. 2 – т. 24), а {ПЗКn = 1 = т. 9 = [Bi2Sr2Ca3Cu9O2]16+} – на отрезке (т. 5 – т. 23), где:

(41)

(42)

Важно также отметить, что продолжение отрезка{Sr2+ - (ПЗКn = 1 =т. 9 = [Bi2Sr2Ca2Cu3O2]16+)} не пересекается с отрезком (SrO – т. 2) указывая тем самым на отсутствия ПХС, который бы следовал за (ПХС = т. 1) в сторону (Bi2Ca2Cu3O8 = т. 2). Сказанное графически подтверждает, что (ПЗКn(bas) = 1 = т. 9) и (ПХСn(bas) = 1 = т. 1) являются первыми членами в ГС, которой принадлежит (ПХСn(bas) = т. 14 = Bi2Sr18Ca2Cu3O26). Тогда в соответствии с (11) при n(bas) = 3 получим:

(43)

Разработанный способ позволяет достаточно просто рассчитать формулу ГС много компонентных систем ионов ХЭ. Для этого достаточно определить формулу гомологической разницы ∆ и положение базового кластера в искомой ГС. Вычитание максимального количества раз формулы гомологической разницы из формулы базового кластера при условии сохранения в ХС минимального количества катиона, входящего в состав ∆, определяет формулу искомой ГС. В результате рассчитаны формулы ГС четырех систем ионов ХЭ: {Li+ - Fe2+ - (PO4)3-}в направлении Fe2O3, (La3+ - Sr2+ - Ti4+ - O2-) в направлении SrO и (Bi3+-Sr2+-Ca2+-Cu2+-O2-) в направлении Bi2O3: Li12Fe6n + 9(PO4)4n + 10, La2Sr15n - 11Ti6O15n + 4, Bi2Sr8n - 6Ca2Cu3O8n + 2.

Анализ расположения членов одной и той же ГС в геометрических фигурах, которые представляют систему ионов ХЭ, выявил важную особенность: независимо от сложности системы гомологи ХСn = 1 и ХСn > 1 располагаются всегда на разных отрезках.