Homologous series of chemical compounds in the (Ca2+ – Ir4+ – Ir5+ – O2-) system based on the compound Ca5Ir4+Ir5+2O12
Homologous series of chemical compounds in the (Ca2+ – Ir4+ – Ir5+ – O2-) system based on the compound Ca5Ir4+Ir5+2O12
Abstract
This paper presents, for the first time, a method for calculating the formulas of homologous series of chemical compounds in the four-component ion system (Ca2+-Ir4+-Ir5+-O2-) based on the compound Ca5Ir4+Ir5+2O12, a well-known catalyst. For the (Ca2+-Ir4+-Ir5+-O2-) system, three homologous series were calculated for the directions of development towards CaO, IrO2 and Ir2O5: Ca7n - 2Ir4+Ir5+2O7n + 5, Ca5Ir4+5n - 4Ir5+2O10n + 2, Ca25Ir4+5Ir5+14n - 4O35n + 25. The obtained formulas of homologous series of chemical compounds make it possible to determine the formulas of new four-component compounds, which are expected to exhibit catalytic properties superior to those of the known compound Ca5Ir4+Ir5+2O12 for the better. From the point of view of saving expensive iridium, the formula of the homologous series Ca7n - 2Ir4+Ir5+2O7n + 5 deserves attention, which is developing towards CaO.
1. Введение
Известно, что металлы платиновой группы, включая иридий, обладают уникальными свойствами. Так, окислы иридия IrO2, CaIr4+O3, Ca2Ir4+O4, Ca4Ir4+O6 обладают полупроводниковыми свойствами с относительно хорошей стабильностью теплопроводности от температуры . Новое семейство электрокатализаторов в виде окисла пирохлора иридия (Na, Ca)2- x(Ir2 – yMy)O6, где (M = Sb, Zr, Ru, Rh), в частности, соединение Ca2 - xIr2O6∙nH2O проявляет высокую электрокаталитическую активность для выделения кислорода в водных сильно кислотных условиях при ~80 oC с сохранением стабильности структуры , . Авторы работ , обнаружили в кристаллической решетке химического соединения (ХС) Ca5Ir3O12 присутствие ионов Ir4+ и Ir5+ в соотношении ½. Следуя работам , и соблюдая электронейтральность формулы соединение Ca5Ir3O12 правильно записать так: Ca5Ir3O12 ≡ Ca5Ir4+Ir5+2O12. По этой причине, при поиске новых соединений в системе (кальций-иридий-кислород), которой принадлежит соединение Ca5Ir4+Ir5+2O12, с помощью формул гомологических серий (ГС) химических соединений, необходимо эту систему химических элементов (ХЭ) представлять как четырехкомпонентную систему ионов (Ca2+-Ir4+-Ir5+-O2-) в виде треугольной пирамиды . Ранее в работах , представлен способ расчета формул ГС четырехкомпонентных систем ионов ХЭ в обобщенном виде (Aa+-Bb+-Dd+-Cc-).
Основы разработанного в исследованиях , , способа расчета формул ГС заключаются в следующем:
1. При расчете рассматриваются все возможные последовательно протекающие реакции химического взаимодействия элементарных и более сложных химических компонент системы, начиная со взаимодействия катионов между собой и катионов с анионом. Геометрические особенности фигур, треугольника и треугольной пирамиды, представляющих систему ионов, позволяют из всего набора реакций выделить те, которые принадлежат одной и той же ГС, что описывается определенной формулой.
2. В системах, представленных треугольником или треугольной пирамидой, химическое взаимодействие двух каких-либо химических реагентов изображается отрезком прямой. Продукты этой реакции также находятся на том же отрезке. Следовательно, если в этих геометрических фигурах пересекаются несколько отрезков, представляющих разные пары реагентов, то можно заключить, что в точке пересечения находится общее для этих пар реагентов новое более сложное по сравнению с реагентами ХС или заряженный кластер (ЗК). Причем формула кластера, находящегося в точке пересечения этих отрезков, однозначно определяется всеми уравнениями реакций, которые соответствуют всем пересекающимися отрезкам. Из этого также следует, что все ХС и ЗК рассматриваемой системы ионов ХЭ, располагаются только в точках пересечения отрезков, представляющих взаимодействия различных пар реагентов.
3. В формировании ГС участвуют следующие реакции химического взаимодействия: ЗКn + Cc- → ХСn, и (ЧХСn + положительно заряженный ион ХЭ → ЧЗКn + 1), где ЧХС и ЧЗК – четырехкомпонентные ХС и ЗК, соответственно, n ≥ 1.
4. Любое ХСn является членом какой-либо ГС с n ≥ 1.
5. Формулы соседних гомологов, ХСn + 1 и ХСn, а также ЗКn + 1 и ЗКn, принадлежащих одной и той же ГС, отличаются на одну и ту же формулу, называемую гомологической разницей, Δ: (ХСn + 1 – ХСn = Δ) , а также (ЗКn + 1 – ЗКn = Δ).
6. Тогда (ХСn = ХСn = 1 + k∙Δ) и (ЗКn = ЗКn = 1 + k∙Δ), где k ≥ 0, k – целые числа.
7. При расчете формулы ГС, которой принадлежит какое-либо известное ХС, называемое базовым кластером, (ХСn(bas)), используется выражение (ХСn = 1 = ХСn(bas) – kbas∙Δ). Причем, для базового кластера (nbas = kbas + 1) и для любого гомолога (n = k + 1). Тогда формула ГС, соответствующая формуле любого гомолога ХСn, выглядит так: (ХСn = ХСn(bas) + (n – 1 – kbas∙Δ).
8. В работах , показано, что ГС в четырех- и пятикомпонентных системах могут развиваться только в сторону двухкомпонентных ХС (ДХС), а в сторону трехкомпонентных ХС (ТХС) – не могут развиваться.
9. В работах , показано, что расположение гомологов ХСn = 1 и ХСn > 1, а также гомологов ЗКn = 1 и ЗКn > 1 разделено кластерами, формулы которых определяются точками пересечения отрезков, ограниченных компонентами системы, где формируется рассматриваемая ГС.
Очевидно, что экспериментально термодинамически и кристаллохимически определить законы формирования ГС химических соединений невозможно. Однако, как показано в работах [11], [12], если использовать геометрические особенности треугольника и треугольной пирамиды для представления системы ионов ХЭ, то при рассмотрении всех возможных химических взаимодействий компонентов системы удается выявить те реакции, которые участвуют в формировании ГС.
Как указано в работах [6], [7], надежная экспериментальная проверка достоверности способа расчета ГС многокомпонентных систем в литературе отсутствуют (так как это финансово затратное мероприятие). Однако при использовании разработанного в [8], [10] способ расчета формул ГС была получена формула ГС (M+4Ti4+n + 1O2-2(n + 2)) для следующих конкретных систем ионов ХЭ: (M+-Ti4+-O2-), где M+ ≡ ≡ Li+, K+, Na+. Причем формула ГС (M+4Ti4+n + 1O2-2(n + 2)) полностью совпадает с формулой, полученной на основе эксперимента [16]. Это говорит о справедливости разработанного в работах [6], [8], [10] принципов расчета формул ГС многокомпонентных систем ионов ХЭ.
Цель работы: рассчитать формулы ГС системы (Ca2+-Ir4+-Ir5+-O2-) на базе четырехкомпонентного соединения Ca5Ir4+Ir5+2O12.
2. Основная часть
2.1. Система (Ca2+ - Ir4+ - Ir5+ - O2-)
В данной работе кластер Ca5Ir4+Ir5+2O12 , является базовым, (ЧХСn(bas) = т. 1 = Ca5Ir4+Ir5+2O12). Образование базового кластера (ЧХСn(bas) = т. 1 = Ca5Ir4+Ir5+2O12) можно описать следующим образом – рис. 1:
Формулы кластеров в виде т. 5, т. 6 и т. 7, ограничивающие плоскости (т. 5 – Ca2+ – O2-), (т. 6 – (Ir4+ – O2-) и (т. 7 – Ir5+ – O2-), в которых формируются четырехкомпонентные ГС (ЧГС), определятся следующими уравнениями:
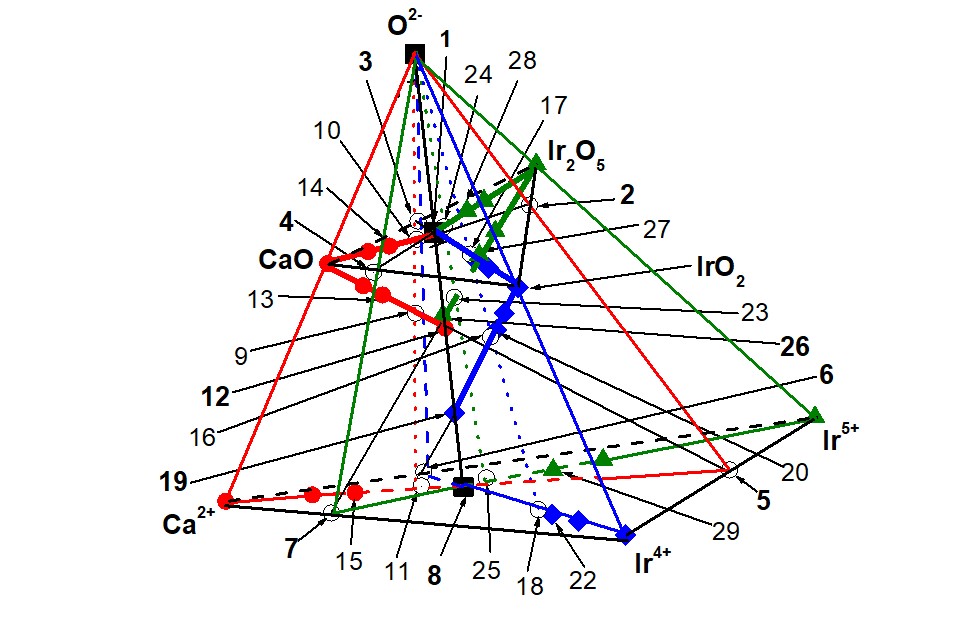
Рисунок 1 - Система (Ca2+ - Ir4+ - Ir5+ - O2-)
т. 3 = ЧХСn(bas) = 1 = Ca5Ir5+2O10, т. 4 = ТХСn(bas) = Ca10Ir4+2O14,
т. 5 = [Ir4+Ir5+2]14+, т. 6 = [Ca5Ir5+2]20+, т. 7 = [Ca5Ir4+]14+, т. 8 = [Ca5Ir4+Ir5+2]24+,
т. 9 = [Ca7Ir4+Ir5+2O7]14+, т. 10 = Ca7Ir4+Ir5+2O14, т. 11 = [Ca7Ir4+Ir5+2]28+,
т. 12 = ЧЗКn(bas) = [Ca5Ir4+Ir5+2O5]14+, т. 13 = [Ca12Ir4+Ir5+2O12]14+,
т. 14 = Ca12Ir4+Ir5+2O19, т. 15 = [Ca12Ir4+Ir5+2]38+, т. 16 = [Ca5Ir4+5Ir5+2O10]20+,
т. 17 = Ca5Ir4+11Ir5+2O32, т. 18 = [Ca5Ir4+11Ir5+2]42+, т. 19 = [Ca5Ir4+Ir5+2O2]20+ = ЧЗКn(bas),
т. 20 = [Ca5Ir4+Ir5+2O2]20+, т. 21 = Ca5Ir4+6Ir5+2O22, т. 22 = [Ca5Ir4+6Ir5+2]44+,
т. 23 = [Ca25Ir4+5Ir5+14O35]70+, т. 24 = Ca25Ir4+5Ir5+14O70, т. 25 = [Ca25Ir4+5Ir5+14]140+,
т. 26 = [Ca5Ir4+Ir5+2O5]14+, т. 27 = [Ca25Ir4+5 Ir5+24O60]70+,
т. 28 = Ca25Ir4+5 Ir5+24O95, т. 29 = [Ca25Ir4+5 Ir5+24]190+.
Трехкомпонентные заряженные кластеры в виде т. 5, т. 6 и т. 7, состоящие только из катионов, при взаимодействии друг с другом образуют ЧЗКв виде т. 8, который взаимодействуя с анионом участвует в образовании базового кластера (ЧХСn(bas) = т. 1 = Ca5Ir4+Ir5+2O12) – рис. 1:
Боковыми гранями треугольной пирамиды, представляющей четырехкомпонентную систему (Ca2+ - Ir4+ - Ir5+ - O2-), являются трехкомпонентные системы (Ir4+ – Ir5+ – O2–), (Ca2+ – Ir5+ –O2–) и (Ca2+ – Ir5+ – O2–), которым принадлежат ТХС в виде (Ir4+Ir5+2O7 = т. 2), (Ca5Ir5+2O10 = т. 3) и (Ca5Ir4+ O7 = т. 4), участвовавшие согласно (1) в реакции образования (Ca5Ir4+Ir5+2O12 = ЧХСn(bas) = т. 1).
Для определения формулы ветви ЧХС в ГС по формуле (ЧХСn = ЧХСn(bas) – kbas∙Δ) необходимо определить формулу гомологической разницы Δ и значение kbas, где (kbas ≥ 0) и kbas – целые числа.
2.2. Подсистема (Ca2+ - т. 5 - O2-). Направление ГС-1 – CaO
Для ГС-1 эта задача будет решена так:
Так как (k(bas) ≥ 0), (ЧХСn = 1 = ЧХСn(bas) – k(bas)∙Δ) и (n(bas) = k(bas) + 1), то выясняется, что при определении ЧХСn = 1, вычитать формулу (Δ = Ca7O7) из формулы (Ca5Ir4+Ir5+2O12 = ЧХСn(bas) = т. 1 ) нельзя. Следовательно, k(bas) = 0 и n(bas) = 1. Тогда получим:
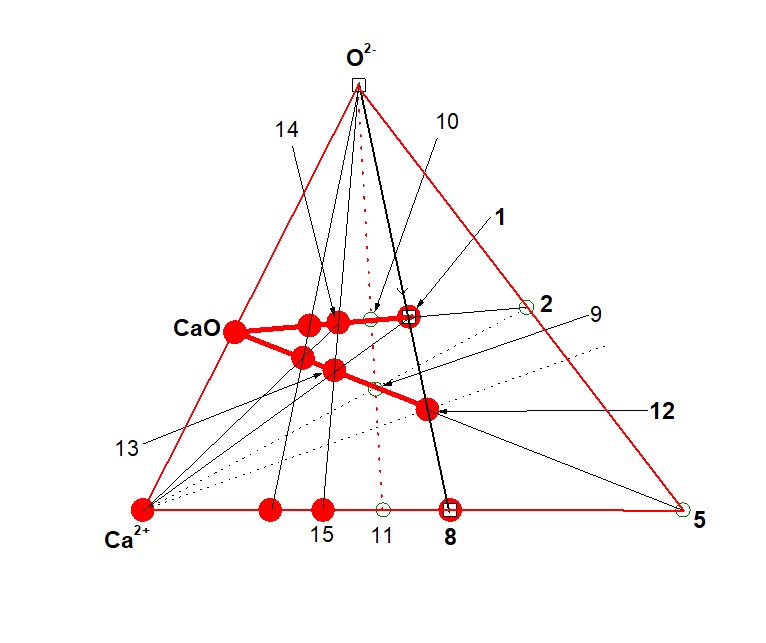
Рисунок 2 - Подсистема (Ca2+ – т. 5 – O2–). Направление ГС-1 – CaO
т. 5 = ([Ir4+Ir5+2]14+, т. 8 = [Ca5Ir4+Ir5+2]24+,
т. 9 = [Ca7Ir4+Ir5+2O7]14+, т. 10 = Ca7Ir4+Ir5+2O14,
т. 11 = [Ca7Ir4+Ir5+2]28+, т. 12 = ЧЗКn(bas) = [Ca5Ir4+Ir5+2O5]14+,
т. 14 = [Ca12Ir4+Ir5+2O12]14+, т. 14 = Ca12Ir4+Ir5+2O19, т. 15 = [Ca12Ir4+Ir5+2]38+.
В формуле (Ca7Ir4+Ir5+2O14 = 7CaO + Ir4+Ir5+2O7 = т. 10) отношение CaO/Ir4+Ir5+2O7 = 7, а в формуле (Ca5Ir4+Ir5+2O12 = 5CaO + Ir4+Ir5+2O7 = ЧХСn(bas) = т. 1 ) отношение CaO/Ir4+Ir5+2O7 = 5. Следовательно, кластер (Ca5Ir4+Ir5+2O12 = ЧХСn(bas) = 1 = т. 1 ) расположен на отрезке (т. 10 – т. 2), а кластеры ЧХСn > 1 – на отрезке (т. 10 – CaO) – рис. 2.
В формуле ([Ca7Ir4+Ir5+2O7]14+ = 7CaO + [Ir4+Ir5+2]14+ = т. 9) отношение CaO/[Ir4+Ir5+2]14+ = 7, а в формуле ([Ca5Ir4+Ir5+2O5]14+ = 5CaO + [Ir4+Ir5+2]14+ = ЧЗКn(bas) = т. 12 ) отношение CaO/[Ir4+Ir5+2]14+ = 5. Следовательно, кластер ([Ca5Ir4+Ir5+2O5]14+ = ЧЗКn(bas) = 1 = т. 12 ) расположен на отрезке (т. 9 – т. 5), а кластеры ЧЗКn > 1 – на отрезке (т. 9 – CaO) – рис. 2.
Кластер в виде т. 9 находится на пересечении отрезков, (Ca2+ – т. 2) и (CaO – т. 5), а кластер в виде т. 10 – на пересечении отрезков (CaO – т. 2) и (т. 9 – O2-) – рис. 2:
Итак, в системе (Ca2+ – т. 5 – O2–) кластером, разделяющим ЧЗКn = 1 и ЧЗКn > 1, оказывается кластер в виде т. 9, а кластером, разделяющими ЧХСn = 1 и ЧХСn > 1 – кластер в виде т. 10 – рис. 2.
2.3. Подсистема (Ir4+ - т. 6 - O2-). Направление ГС-2 – IrO2
Для ГС-2 эта задача будет решена так:
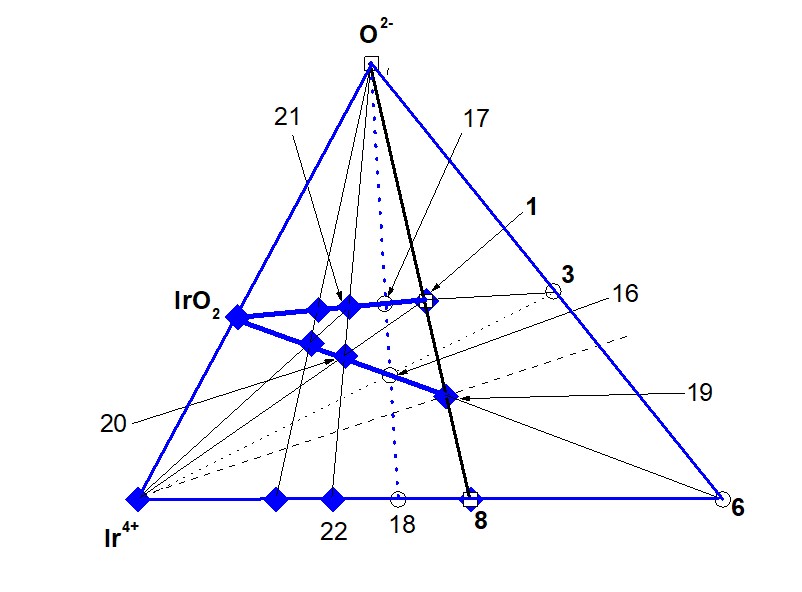
Рисунок 3 - Подсистема (Ir4+ – т. 6 – O2–). Направление ГС-2 – IrO2
т. 6 = [Ca5Ir5+2]20+, т. 8 = [Ca5Ir4+Ir5+2]24+,
т. 16 = [Ca5Ir4+5Ir5+2O10]20+, т. 17 = Ca5Ir4+5Ir5+2O20,
т. 18 = [Ca5Ir4+11Ir5+2]42+, т. 19 = [Ca5Ir4+Ir5+2O2]20+ = ЧЗКn(bas),
т. 20 = [Ca5Ir4+Ir5+2O2]20+, т. 21 = Ca5Ir4+6Ir5+2O22, т. 22 = [Ca5Ir4+6Ir5+2]44+.
Так как (k(bas) ≥ 0), (ТХСn = 1 = ТХСn(bas) – k(bas)∙Δ) и (n(bas) = k(bas) + 1), то выясняется, что при определении ТХСn = 1, вычитать формулу (Δ = Ir4+5O10) из формулы (Ca5Ir4+Ir5+2O12 = ТХСn(bas) = т. 1) нельзя. Следовательно, k(bas) = 0 и n(bas) = 1. Тогда получим:
В формуле (Ca5Ir4+5Ir5+2O20 = 5IrO2 + Ca5Ir5+2O10 = т. 17) отношение IrO2/ Ca5Ir5+2O10 = 5, а в формуле (Ca5Ir4+Ir5+2O12 = IrO2 + Ca5Ir5+2O10 = ЧХСn(bas) = т. 1 ) отношение IrO2/ Ca5Ir5+2O10 = 1. Следовательно, кластер (Ca5Ir4+Ir5+2O12 = ЧХСn(bas) = 1 = т. 1 ) расположен на отрезке (т. 17 – т. 3), а в кластеры ЧХСn > 1 – на отрезке (т. 17 – IrO2) – рис. 3.
В формуле ([Ca5Ir4+5Ir5+2O10]20+ = 5IrO2 + [Ca5Ir5+2]20+ = т. 16) отношение CaO/[Ca5Ir5+2]20+ = 5, а в формуле (= [Ca5Ir4+Ir5+2O2]20+ = IrO2 + [Ca5Ir5+2]20+ = ЧЗКn(bas) = т. 19 ) отношение IrO2/[Ca5Ir5+2]20+ = 1. Следовательно, кластер ([Ca5Ir4+Ir5+2O2]20+ = ЧЗКn(bas) = 1 = т. 19 ) расположен на отрезке (т. 16 – т. 6), а кластеры ЧЗКn > 1 – на отрезке (т. 16 – IrO2) – рис. 3.
Кластер в виде т. 16 находится на пересечении отрезков, (Ir4+ – т. 3) и (IrO2 – т. 6), а кластер в виде т. 17 – на пересечении отрезков (IrO2 – т. 3) и (т. 16 – O2-) – рис. 3:
Итак, в системе (Ir4+ – т. 6 – O2–) кластером, разделяющим ЧЗКn = 1 и ЧЗКn > 1, оказывается кластер в виде т. 16, а кластером, разделяющими ЧХСn = 1 и ЧХСn > 1 – кластер в виде т. 17 – рис. 3.
2.4. Подсистема (Ir5+ - т. 7 - O2-). Направление ГС-3 – Ir2O5
Для ГС-3 эта задача будет решена так:
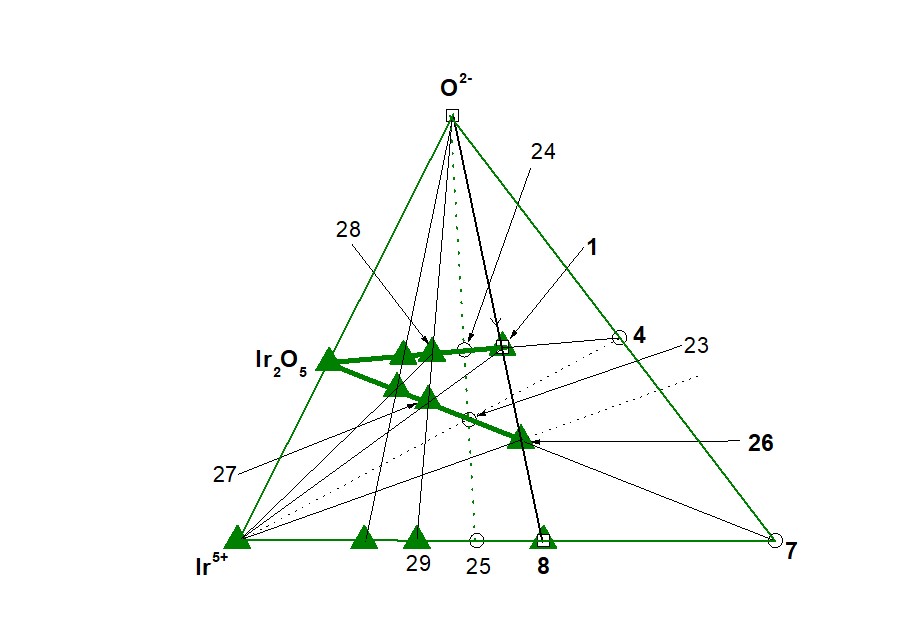
Рисунок 4 - Подсистема (Ir5+ – т. 7 – O2–). Направление ГС-3 – Ir2O5
т. 7 = [Ca5Ir4+]14+, т. 8 = [Ca5Ir4+Ir5+2]24+,
т. 23 = [Ca25Ir4+5Ir5+14O35]70+,
т. 24 = Ca25Ir4+5Ir5+14O70, т. 25 = [Ca25Ir4+5Ir5+14]140+,
т. 26 = [Ca5Ir4+Ir5+2O5]14+, т. 27 = [Ca25Ir4+5 Ir5+24O60]70+,
т. 28 = Ca25Ir4+5 Ir5+24O95, т. 29 = [Ca25Ir4+5 Ir5+24]190+.
Так как (k(bas) ≥ 0), (ТХСn = 1 = ТХСn(bas) – k(bas)∙Δ) и (n(bas) = k(bas) + 1), то выясняется, что при определении ТХСn = 1, вычитать формулу (Δ = Ir5+14O35) из формулы (Ca25Ir4+5 Ir5+10O60 = ТХСn(bas) = т. 1) нельзя. Следовательно, k(bas) = 0 и n(bas) = 1. Тогда получим:
В формуле (Ca25Ir4+5Ir5+14O70 = 7Ir2O5 + 5Ca5Ir4+O7 = т. 24) отношение Ir2O5/ Ca5Ir4+O7 = 7/5, а в формуле (Ca25Ir4+5Ir5+10O60 ≡ Ca5Ir4+Ir5+2O12 = 5Ir2O5 + 5Ca5Ir4+O7 = ЧХСn(bas) = т. 1) отношение Ir2O5/Ca5Ir4+O7 = 1. Следовательно, кластер (Ca25Ir4+5Ir5+10O60 ≡ Ca5Ir4+Ir5+2O12 = ЧХСn(bas) = 1 = т. 1 ) расположен на отрезке (т. 24 – т. 4) – рис. 4.
В формуле ([Ca25Ir4+5Ir5+14O35]70+ = 7Ir2O5 + 5[Ca5Ir4+]14+ = т. 23) отношение Ir2O5/[Ca5Ir4+]14+ = 7/5, а в формуле ([Ca25Ir4+5Ir5+10O25]70+ = 5Ir2O5 + 5[Ca5Ir4+]14+ = ЧЗКn(bas) = = т. 23 ) отношение Ir2O5/[Ca5Ir4+]14+ = 1. Следовательно, кластер ([Ca5Ir4+Ir5+2O5]14+ = ЧЗКn(bas) = 1 = т. 26 ) расположен на отрезке (т. 23 – т. 7), а кластеры ЧЗКn > 1 – на отрезке (т. 23 – Ir2O5) – рис. 4.
Кластер в виде т. 23 находится на пересечении отрезков, (Ir5+ – т. 4) и (Ir2O5 – т. 7), а кластер в виде т. 24 – на пересечении отрезков (Ir2O5 – т. 4) и (т. 23 – O2-) – рис. 4:
Итак, в системе (Ir5+ – т. 7 – O2–) кластером, разделяющим ЧЗКn = 1 и ЧЗКn > 1, оказывается кластер в виде т. 23, а кластером, разделяющими ЧХСn = 1 и ЧХСn > 1 – кластер в виде т. 24 – рис. 4.
3. Заключение
Закономерное обогащение гомологов одной и той же ГС двухкомпонентным ХС при неизменности гомологической разницы Δ для данной ГС должно привести к закономерному изменению кристаллической решетки ее членов. В совокупности все это должно привести к закономерному изменению фундаментальных характеристик ХС-гомологов этой ГС. Примером работоспособности разработанного в [6], [8], [10]способа расчета формул ГС является совпадение формулы ГС (M+4Ti4+n + 1O2-2(n + 2)) системы (M+-Ti4+-O2-), где M+ ≡ Li+, K+, Na+, полученной расчетом в [10] и экспериментально в [16]
Формулы четырехкомпонентных ГС системы (Ca2+ – Ir4+ – Ir5+ – O2-) получены с помощью упрощенного способа расчета. Развитие рассчитанных ГС происходит в трех направлениях: в сторону CaO, IrO2 и Ir2O5. Гомологические серии формируются в подсистемах (Ca2+ – [Ir4+Ir5+2]14+ – O2-), (Ir4+ – [Ca5Ir5+2]10+ – O2-) и (Ir5+ – [Ca5Ir4+]14+ – O2-). Как выяснилось, в системе (Aa+ – Bb+ – Dd+ – Cc-) вообще, и в системе (Ca2+ – Ir4+ – Ir5+ – O2-), в частности, всем подсистемам, где формируются трех- и четырехкомпонентные ГС, характерно раздельное расположение кластеров с n = 1 и n > 1. Во всех трех выше указанных подсистемах кластеры ЧХСn = 1 и ЧХСn > 1 разделены так, что ЧХСn = 1 находятся на отрезках (Ca7Ir4+Ir5+2O14 – Ir4+Ir5+2O7), (Ca5Ir4+5Ir5+2O20 – Ca5Ir5+2O10) и (Ca25Ir4+5Ir5+14O70 – Ca5Ir5+2O10), соответственно. При этом, кластеры ЧЗКn = 1 и ЧЗКn > 1 также разделены так, что ЧЗКn = 1 находятся на отрезках (CaO – [Ca7Ir4+Ir5+2O7]14+), (IrO2 – [Ca5Ir4+5Ir5+2O10]20+) и (Ir2O5 – [Ca25Ir4+5Ir5+14O25]70+, соответственно.
Согласно пункту 3 во Введении, если n = 1, то продолжение отрезка (положительно заряженный ион ХЭ – ЧЗКn = 1) не пересекается с отрезком, на котором располагаются все ЧХСn ≥ 1.
